Every number that we encounter in our daily lives cannot be an absolute whole number. For example, if a pizza is divided into 6 slices, we may say that each piece is one-sixth of the entire pizza. Therefore, it is evident that we may have to deal with parts of a whole, sections of a whole, and fractions. The phrase “fraction” refers to the components of a whole object. In this article, we will look at the seven types of fractions in mathematics along with their operations and properties.
What exactly are fractions?
Let’s start with a definition of fractions. The term “fraction” refers to a numerical amount that is a portion of the whole. With the help of the examples given below, you can grasp the concepts of fractions better.
Example 1:
Assume we have a huge cake that has been sliced into 8 equal slices. Then, each slice is merely 1/8th of the entire quantity of cake. 1/8 is a fraction in this context.
Example 2:
Fractions as a part of a circle.
A circle is a geometric form. The circle as shown below represents the whole.
What fractions do you obtain when you divide this circle into equal sections? Let’s look at the images below to understand!
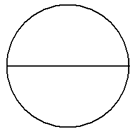
The whole circle has been divided into 2 equal parts.
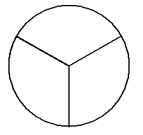
This whole circle has been split into 3 equal parts.
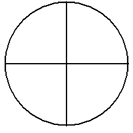
The circle has been divided into 4 equal parts.
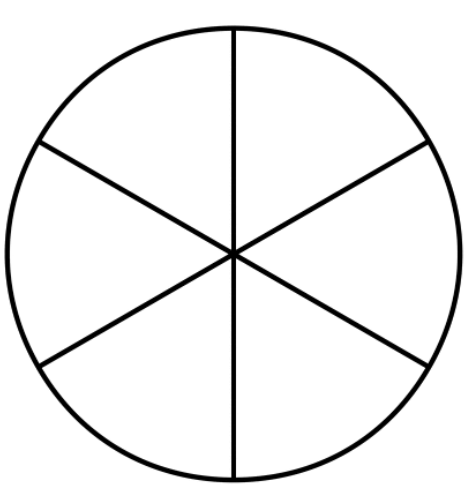
This circle has been divided into 6 equal parts.
You can shade a portion of a circle to name a specific part of the whole as shown below.
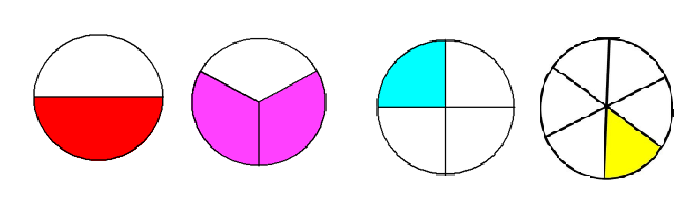
The above images depict the fractions 1/2, 2/3, 1/4 and 1/6.
Parts of a Fraction
The numerator is the top part of the fraction, while the denominator is the bottom component. For example, in the fraction 2/5, 2 is the numerator and 5 is the denominator. The last component of a fraction is the line that separates the numerator and denominator.
Real-World Applications of Fractions and Its Types
Fractions are used in several aspects of daily life. Here are some real-world examples of fractions:
Eating out:
Consider the last time you went to a restaurant with friends and the waitress brought you a single bill. Fractions are used to divide the sum among the pals.
Shopping:
The last time you went shopping for a new school backpack, everything was half off because of a deal. Thus, you computed the new price using fractions.
Making a recipe:
Some recipes call for 1 or 2 teaspoons sugar and 3 or 4 tablespoons salt. In addition, some recipes provide serving sizes for two people. Thus, if you are creating the same food for three people, you may utilise fractions to alter the components proportionately.
In sports:
Fractions are commonly employed to assess the performance of a certain individual or team.
Fitness:
We utilise fractions to comprehend our body mass index (BMI) and if we are in a healthy weight range.
Beverages:
To produce drinks like mocktails, different fractions of liquids are blended in the appropriate quantities.
Pizza:
Dividing the pizza slices evenly among everyone necessitates the use of fractions.
Photography and videography:
A camera’s shutter speed is computed using fractions.
Tests and exams:
Test and exam scores are typically expressed infractions, such as 18/20 or 45/50.
Medical Prescriptions:
When a person is ill, the doctor will prescribe different doses for persons of different sizes. A full-grown adult may take 500mg, whilst a youngster may ingest 250mg, which is half of the adult dose.
Progress or decline:
Any project’s progress or decline may be measured with fractions. For example, a given product’s sales are down by 25%.
Time:
30 minutes is commonly expressed as half an hour.
Types of Fractions
There are 7 different types of fractions. They are as follows:
Proper Fraction
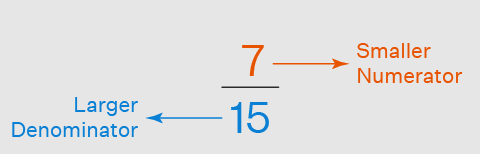
A proper fraction is a fraction in which the numerator is smaller than the denominator, i.e. numerator < denominator. For example, let’s take a fraction 2/5. In this fraction, the numerator is 2 and the denominator is 5. In this fraction, we can see that, the numerator is less than the denominator, that means, 2 < 5. Hence, it is a proper fraction.
Improper Fraction
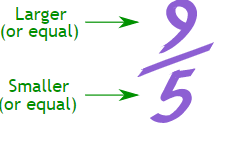
An improper fraction is one in which the numerator is bigger than the denominator, i.e. numerator > denominator. Because the denominator is always equal to one, we can express all natural numbers as fractions. When we simplify an improper fraction, we always get a number that is equal to or higher than 1, but never less than 1. Take, for example, the fraction 7/5. The numerator in this fraction is 7 and the denominator is 5. It is obvious that the numerator is bigger than the denominator in this fraction, as 7 > 5. As a result, it is an improper fraction.
Mixed Fraction
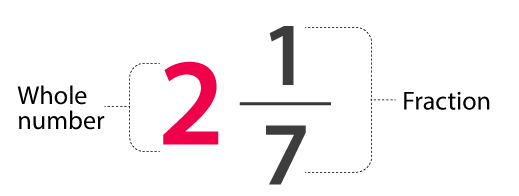
A mixed fraction is a fraction that contains both a natural number and a fraction. It is, in essence, an incorrect fraction. The advantage of a mixed fraction is that it can always be transformed into a fraction. In addition, an incorrect fraction can be converted into a mixed fraction. Mixed fractions are always bigger than one.
Like Fractions
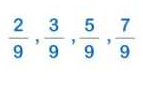
Like fractions are ones that have the same denominator. For example, 1/2, 3/2, 5/2, and 9/2, are like fractions because the denominators of these fractions are the same. So, if we wish to add these similar fractions, we must add all of the numerators and then divide by the denominator, which is the same in all of them. For example, 1/2+ 3/2 + 5/2 + 9/2 = (1+3+5+9)/2 = 18/2 = 9.
Unlike Fractions
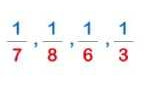
Unlike fractions are those fractions which have unequal denominators or different denominators. Examples of like fractions are 2/3, 1/4, 3/7, 3/5. To simplify unlike fractions, firstly we need to factorise the denominators and then simplify them. Hence, it goes through a lengthy method. For example, we have to add 1/3 and 1/4, then first, we have to find the least common multiple (LCM) of 3 and 4 which is equal to 12. After finding the LCM of denominators, we need to multiply 1/3 by 4 and 1/4 by 3, both in numerator and denominator. Then the fractions will become 4/12 and 3/12. Now if we add the two, then the result comes out to be 7/12.
Equivalent Fractions
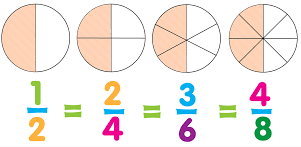
After simplification, when two or more fractions have the same result and represent the same portion of the total, they are termed equivalent fractions and are equal to each other. Examples of such kind of fraction include 1/5 and 5/25, as well as 1/3 and 3/9, wherein the two members within the pairs are equivalent to one another.
Unit Fractions
A unit fraction is a fraction with a numerator of one and a denominator of a positive integer. Unit fractions include 1/2, 1/5, 1/8, and so on.
Operations of Fractions
Calculating with fractions differs from calculating with whole numbers. So, let us go over the processes for executing the different mathematical operations on fractions in detail.
Adding Fractions
To combine two or more fractions with the same denominator, just add the numbers in the numerator while keeping the denominator constant.
For example:
To add the fractions 1/5 and 14/5, you need to simply add the numerators. Thus, the sum of the two fractions is 15/5, which is 3.
But what if the denominators of the fractions are different? To add two or more fractions with various denominators, first, determine the LCM of the denominators and make the denominator the same across all fractions.
Once you’ve determined the LCM, multiply the denominator by the multiplier for each fraction until the denominator equals the LCM. At the same time, to keep the value of the fraction constant, you also need to multiply the numerator of the fraction with the same multiplier. Repeat this operation for all the fractions so that all the fractions have the same denominator. Then, add the fractions.
For example:
To add the fractions 1/5 and 4/7, first, calculate the LCM of the denominators. Here, the LCM is 35. The following steps represent the calculation after this.
1/5*7= 7/35
4/7*5= 20/35
The sum= 7/5+20/35=27/35
Subtracting Fractions
To subtract fractions with the same denominator, subtract the numerator while keeping the denominator constant. Consider the following example:
8/7-2/7
=(8-2)/7=6/7
If you want to subtract the fractions with different denominators, follow the same steps that we did for adding the fractions, and in the last step, subtract the numerators.
For example:
To LCM the fractions 4/5 and 1/2, is 10. Thus,
4/5*2=8/10
1/2*5=5/10
The difference=8/10-5/10=3/10
Multiplying Fractions
Multiplying fractions is an easy task. When multiplying two or more fractions, the numerator of the solution is the product of all fractions’ numerators and the denominator of the solution is the product of all fractions’ denominators. Consider the following example:
Multiply 4/5 and 8/3
The Product= 4*8/5*3
=32/15=2 2/15
Dividing Fractions
The technique for dividing fractions follows the same procedures as the method for multiplying fractions, with one exception. The numerator and denominator of the second fraction are interchanged. This step converts the divide operation into a multiplication operation.
Consider the following example:
Solve 2/5 ÷ 5/8
To solve this example, interchange the numerator and denominator of the second fraction. Thus, 5/8 becomes 8/5. Then, replace the division symbol with the multiplication symbol.
Solving the equation as a multiplication operation
2/5÷5/8
=2/5*8/5
=2*8/5*5
=16/40
Comparing Fractions
Three different methods can be used to compare fractions.
Case 1: When the denominators are the same but the numerators are not.
In this case, the fraction with the larger numerator is the bigger fraction.
For Example:
Compare 5/8 and 7/8
Answer: 5/8<7/8 because 5<7
Case 2: When the numerators are the same, but the denominators are not. In this case, the fraction with the smallest denominator is the bigger fraction.
For Example:
Compare 13/9 and 13/5
Here, 9>5. Therefore, 13/5 is smaller than 13/9
Case 3: When the numerators and denominators of the provided fractions differ, we must convert the fractions to like fractions by calculating the LCM of the denominators. As illustrated above, the resulting similar fractions are then compared.
For Example:
Compare 2/5 and 3/7
LCM of 5 and 7 is 35
Therefore the fraction becomes:
2/5*7=14/35
3/7*5=15/35
Then compare ./35 and 15/35. As 15/35 is greater, 3/7 is greater than 2/5
Please note that while comparing fractions, there is one general rule that you can follow. The rule states that “the greater the numerator, the larger the fraction, and the smaller the fraction, the larger the denominator.”
Properties of the Different Types of Fractions
The different properties for multiplication and addition of fractions are mentioned in the table below. It is important to note that all types of fractions follow each of these properties.
Each feature is discussed in detail below, with examples.
| Property | Addition | Multiplicaiton |
| Associative | a+(b+c)= (a+b)+c | a.(b.c)= (a.b).c |
| Communicative | a+b= b+a | a.b= b.a |
| Identity | a+0= a | a.1=a |
| Inverse | a+(-a)= 0 | a.(1/a)= 1 |
| Distributive property | a.(b+c)= a.b+ a.c |
Associative Property
Associative Property of Addition
As with numbers and integers, the associative property of the addition of fractions is as follows:
a/b+(c/d+e/f)=(a/b+c/d)+e/f
For Example:
1/2+(1/5+1/3)=(1/2+1/5)+1/3
1/2+8/15= 7/10+1/3
31/30=31/30
In this example, the answer on both the right hand side (RHS) and left hand side (LHS) is the same. Hence, we can say that fractions follow the associative property of addition.
Associative Property of Multiplication
The associative property of multiplication in fractions is written as follows:
a/b*(c/d*e/f)=(a/b*c/d)*e/f
For Example:
2/5*(1/5*3/2)=(2/5*1/5)*3/2
2/5*3/10=2/25*3/2
6/50=6/50
In this example, the answer will be 6/50 on both the LHS and RHS sides. Hence we can say that fractions follow the associative property of addition.
Commutative Property
Commutative Property of Addition
The communicative property of addition in fractions is given by:
a/b+c/d=c/d+a/b
For Example:
1/2+1/4=1/4+1/2
3/4=3/4
In this example, the answer is 3/4 on both the RHS and LHS sides. Hence we can say that fractions follow the communicative property of addition.
Commutative Property of Multiplication
The Communicative property of multiplication is given as:
a/b*c/d=c/d*a/b
For Example:
7/2*4/3=4/3*7/2
14/3=14/3
In this example, the answer on both the LHS and RHS sides is the same. Hence, we can say that fractions follow the communicative property of multiplication.
Identity Propert
Identity Property of Addition
The identity property states that the addition of zero to any fraction gives the fraction itself. It is written as:
a/b+0=a/b
For Example:
6/5+0=6/5=1 1/5
Identity Property of Multiplication
The identity property of multiplication states that any fraction multiplied by 1 gives the fraction itself. This is written as:
a/b*1=a/b
For Example:
6/5*1=6/5=1 1/5
Inverse Property
Identity Property of Addition
The identity property states that when a fraction is added to the inverse of itself the result is 0. This is written as:
a/b+ (-a/b)=0
For Example:
7/8+(-7/8)=0
3/5+(−3/5)=0
Identity Property of Multiplication
This property states that when a fraction is multiplied with the inverse of itself the result is 1. It is written as:
a/b*b/a=1
For Example
3/5*5/3=1
1/5*5=1
Distributive Property
According to the distributive property of fractions:
a/b*(c/d+e/f)=a/b*c/d+a/b*e/f
For Example:
3/5(2/4+1/5)=(3/5×2/4)+(3/5×1/5)
3/5*7/10=3/10+3/25
21/50=21/50
In this example, the answer is 21/50 on both the LHS and RHS sides. Hence, we can say that fractions follow the distributive property.
Summing It Up!
As fractions are constantly used in daily life, it is important to learn and understand the concept in depth. We hope that this article has helped you understand the different types of fractions, their operations, and properties.
For more interesting Math lessons visit the Podium School Blog.
FAQs
How to convert fractions into decimal numbers?
Typically, this conversion is carried out using two different methods:
The first method involves long division. In this process, you divide the numerator by the denominator. For example, the fraction 13/67 is 0.194 in decimal form.
The second method involves changing the denominator to a power of ten (such as 10, 100, 1000, etc). When the fraction has powers of 10 in the denominator, you can easily discover the decimal value if it is transformed. For example, to convert 2/5 into its decimal form, first, multiply both the numerator and denominator by 2. The resulting fraction is 4/10, which in decimal form is 0.4.
How to convert fractions into percentages?
To convert a fraction to a percentage, simply multiply the decimal version of the fraction by 100. Here are a few examples to help you learn how to convert a fraction to a percentage.
Examples
- 5/12 in percentage is= 0.416*100= 41.66%
- 126/267=0.471*100= 47.1%
For more examples and practice problems, refer to the document linked below.
A table with fraction to percentage conversion
| Fraction | Per cent |
| 1/2 | 50 % |
| 1/3 | 33.33 % |
| 2/3 | 66.67 % |
| 1/4 | 25 % |
| 2/4 | 50 % |
| 3/4 | 75 % |
| 1/5 | 20 % |
| 2/5 | 40 % |
| 3/5 | 60 % |
| 4/5 | 80 % |
| 1/6 | 16.67 % |
| 2/6 | 33.33 % |
| 3/6 | 50 % |
| 4/6 | 66.67 % |
| 5/6 | 83.33 % |
| 1/7 | 14.285714 % |
| 2/7 | 28.571429 % |
| 3/7 | 42.857143 % |
| 4/7 | 57.142858 % |
| 5/7 | 71.428571 % |
| 6/7 | 85.714286 % |
| 1/8 | 12.5 % |
| 2/8 | 25 % |
| 3/8 | 37.5 % |
| 4/8 | 50 % |
| 5/8 | 62.5 % |
| 6/8 | 75 % |
| 7/8 | 87.5 % |
| 1/9 | 11.111111 % |
| 2/9 | 22.222222 % |
| 3/9 | 33.333333 % |
| 4/9 | 44.444444 % |
| 5/9 | 55.555556 % |
| 6/9 | 66.666667 % |
| 7/9 | 77.777778 % |
| 8/9 | 88.888889 % |
| 1/10 | 10 % |
| 2/10 | 20 % |
| 3/10 | 30 % |
| 4/10 | 40 % |
| 5/10 | 50 % |
| 6/10 | 60 % |
| 7/10 | 70 % |
| 8/10 | 80 % |
| 9/10 | 90 % |
Why do you have to reduce fractions?
You should always reduce fractions into their simplest forms because it is the proper notation. Furthermore, in this form, the fraction is much easier to recognize. For instance, you would be able to easily recognise 1/4 but not 16/ 64.
What is 1/7 as a per cent?
To find 1/7 as a per cent, begin by dividing 1 by 7.
1/7 = 0.143
Then, multiply the above-obtained decimal by 100,
0.143 × 100 = 14.3 %
Thus, the fraction 1/7 is equivalent to 14.3 per cent.
Is it true that all fractions are less than one?
No, not all types of fractions are smaller than one. Proper fractions are those that are higher than 0 but less than 1. In other words, their denominator is smaller than their numerator. Improper fractions, on the other hand, are always equal to one or more than one. This implies that their numerator exceeds or equals their denominator.
How can you multiply fractions with whole numbers?
To multiply fractions with whole numbers, first, express the whole number in fraction form by putting 1 in the denominator, and then use the standard fraction multiplication technique. For instance, let us multiply 5/9 by 3. Here, 3 is a whole number, therefore write it as 3/1. Then, multiply 5/9 and 3/1 = 15/9 = 5/3= 1 2/3
How to convert a mixed fraction into an improper fraction?
A mixed fraction can also be written as an improper fraction. To do so, follow the procedures outlined below. For example, look at the mixed fraction 2 4/5. Here, 2 is the full number, 4, is the numerator, and 5, is the denominator. Follow the following steps to convert the fraction into an improper fraction.
1: Multiply the mixed fraction’s denominator by the whole number component.
2: Then, add the numerator from the product obtained in step 1.
3: Finally, in the numerator/denominator form, write the improper fraction with the total produced in step 2.
Therefore, the answer for the example will be 14/5. You may refer to the video linked below for more examples.
How to convert an improper fraction into a mixed fraction?
An improper fraction is one that cannot be simplified further because the numerator is more than or equal to the denominator. 17/5, for example, is an improper fraction. The steps mentioned below will help you convert an improper fraction to a mixed fraction.
1: First, divide the denominator by the numerator.
2: Then, determine the remainder.
3: Lastly, arrange the numbers as follows: quotient, remainder/divisor fraction.
The video linked below will help you understand the steps better.
Share with your friends

