- Properties of Multiplication
- What Are The 3 Steps To Multiplying Fractions?
- Multiplying Fractions with Whole Numbers
- How Do You Multiply Fractions With Different Denominators?
- Fractions with Mixed Numbers Multiplication
- Improper Fractions of Multiplication
- Dividing Fractions
- Division in Fractions
- Division with Whole Number Fractions
- Dividing Fractions with Decimals
- Two Ways of Dividing Fractions
- Frequently Asked Questions
- Conclusion
The Difference between Arithmetic and simple mathematics is confusing to people including kids. Arithmetic is a branch of mathematics that only deals with the study of numbers. Maths includes everything. The basic or the fundamentals of Mathematics are addition, subtraction, multiplication, and division.
Many cases talk about their experiences of kids loving addition and subtraction. But, when it came to multiplication it did not favor them much. Further in this article, we will put our focus on multiplication and division of fractions.
Before moving ahead with the topic the kids must know what is multiplication? Multiplication is denoted by the symbol ‘x’ or by an asterisk. In simple, the multiplication of whole numbers can be said as repeated addition. We could say that the multiplication of two numbers is the same as adding many copies to them.
Read more about it at: https://en.wikipedia.org/wiki/Multiplication
The simple theory of multiplication is as follows:-
3×4=12, when broken down it, will look 4+4+4=12. This is the basics of multiplication.
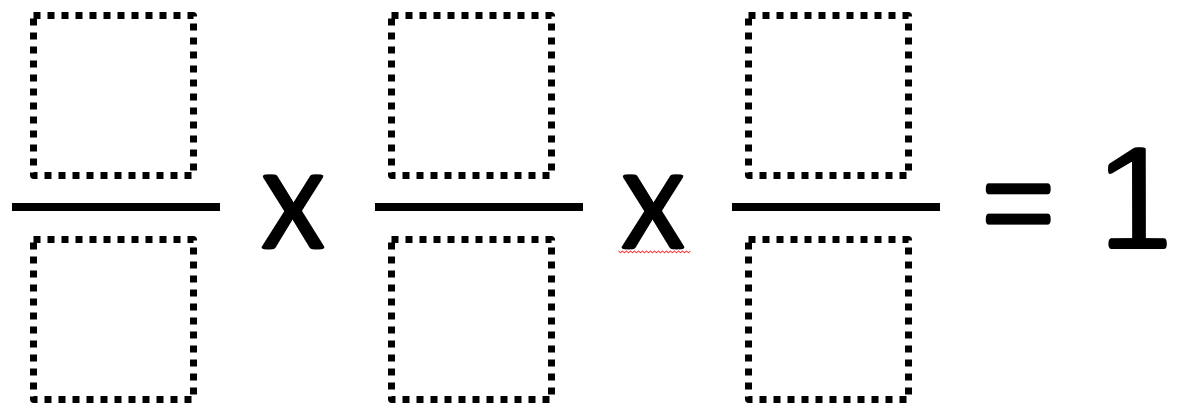
Properties of Multiplication
There are various properties of multiplication but, only three of them are considered important. These three properties are highly used in major parts of the world. The three main properties of multiplication are as follows:-
- Commutative multiplication
- Associative multiplication
- Identity multiplication
These are the three main properties of multiplication.
Commutative multiplication
This property of multiplication says that just changing the order of the factor does not change the product. Here is an example:
4×3=3×4
Multiplying both sides would give the same result. The first paragraph contains an example for this.

Associative multiplication
These properties of multiplication say that changing the group of factors does not change the product. In fact, the product for three or more numbers will remain the same. But, there are certain terms and conditions for this. Here is an example:-
(2×3) x 4= 2 x (3×4)
Solve “=” first. Solving the first part will result in the following:
(2×3) x 4
=6×4
=24
Now, we will move towards the right-hand side of the problem. Follow the same process as in the first part.
2 x (3×4)
=2 x 12
= 24
Moreover, we can see that both sides equal 24 as the final answer. In fact, we did not even multiply them by the same number. Multiply first half by 2 and 3, and 3 and 4 in the right side.
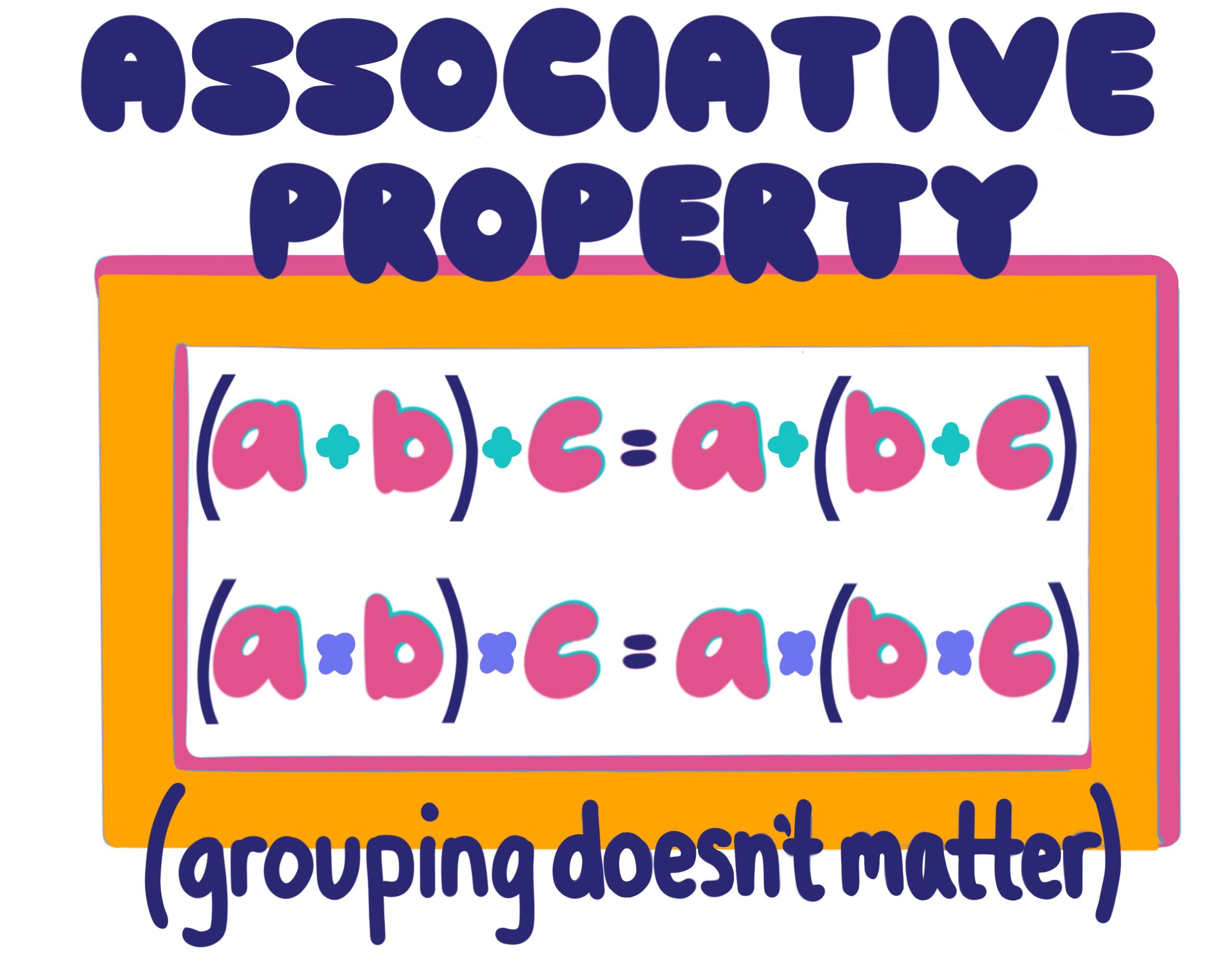
Identity multiplication
This is the simplest property of multiplication. In fact, this property of multiplication says that the product of 1 or any number is that number. Moreover, any number multiplied by 1 will be the original number. Here is an example for you:-
8×1=8
Additionally, it does not matter if 1 comes before or after the consequence will be the same. Here is another example for the same:-
1×8=8
Three highly used and common properties of multiplication are –
Read more about it at: https://www.khanacademy.org/math/cc-sixth-grade-math/cc-6th-factors-and-multiples/properties-of-numbers/a/properties-of-multiplication

What Are The 3 Steps To Multiplying Fractions?
In mathematics, fractions are part of the Arithmetic branch. A fraction consists of a number that expresses a quotient. Moreover, this quotient includes a numerator which is dividing the denominator.
Proper fractions are those in which the numerator is less than the denominator. Improper fractions are those in which the numerator is greater than the denominator. Mixed factors are sums of whole numbers and proper fractions.
You can also add, subtract, or divide a fraction and multiply it. To multiply fractions, one can do it in three simple steps.
Read more about multiplication at: https://www.cuemath.com/numbers/multiplication/

Steps To multiplying fractions:-
- Simply multiply the top numbers. They are numerators.
- Multiply the bottom ones after numerators. These lower ones are denominators.
- If necessary, simplify the fraction.
There is a simple example for multiplication fraction below:-
1/2 x 2/5
First, Multiply the top numbers or numerators.
1/2 x 2/5 = 1×2 =2 (numerator answer)
Second, Multiply bottom numbers or denominators.
1/2 x 2/5 = 1x 2/2×5 = 2/10
Thirdly, if the final result can be simplified into short-form then just simplify it if possible.
2/10= 1/5
The simplification is used with various techniques for the kids to understand better. There is the pizza method, pen, and paper method, the rhyme method, and many more.
Read more about it at: https://www.mathsisfun.com/fractions_multiplication.html#:~:text=There%20are%203%20simple%20steps%20to%20multiply%20fractions&text=Multiply%20the%20top%20numbers%20
Multiplying Fractions with Whole Numbers
Fractions and multiplications can be done with various numbers and types. The same way fraction with whole numbers becomes slightly different but, easy. In fact, it is one of the easiest ways to solve a whole number fraction.
The example for a whole number with a fraction is given below:-
5 x 2/3 here 5 will be counted as 5/1
2/3 x 5/1
Firstly, again we have to follow the first step to multiply the numerators.
2 x 5 will be the multiplication for the numerator and 3 x 1 will be for the denominator.
So, the final answer to them would be 10/3.
In fact, the same can be in another way where we do not take any denominator under a whole number. But, that might be slightly confusing for the kids to understand fractions at this age. Moreover, there is multiplication with mixed fractions as well. Overall, there might be various types but, the steps for them remain the same.
Read more about it at: https://www.mathsisfun.com/fractions_multiplication.html

How Do You Multiply Fractions With Different Denominators?
Multiplying fractions with numerators is quite easy but when it comes to denominators that become quite tough. This is especially for the kMultiplying fractions with numerators is easy, but denominators are quite tough. This is especially true for kids who are in the fourth-seventh grade. We know that in every fraction, there is a top number and a bottom number to deal with.
The numerator in the fraction tells us how many units we have of a whole. On the other hand, the denominators tell us how many units make up the whole. For example, if we take 2/3, 2 here is the numerator and 3 is the denominator.
We can see that there are two units as a whole, but when it comes to a fraction that is not the case. Firstly, to multiply fractions the basic way has been discussed above. Additionally, fractions will be given on both sides and they will need to be multiplied. In fact, the multiplication sequence will be numerator x numerator and denominator x denominator.
Read more about it at: https://study.com/academy/lesson/how-to-multiply-fractions-with-unlike-denominators.html/
Steps to Multiply Fractions with Different Denominators
Unlike denominators is also very easy to multiply. One can easily do a simple multiplication with unlike denominators. The steps to do so are quite the same as multiplication of like fractions. Below is an example of the multiplication of fractions with unlike denominators.
Example: Multiplication fraction of 4/12 x 16/24
There are two different methods to solve the above-mentioned problem. The first one is given below:
- Multiply the numerators to make it simple, 4 x 16= 64
2. Follow the same procedure to multiply the denominators, 12 x 24= 288
3. The final answer that we get here by solving the fraction is 64/288. Moreover, this number can be reduced into a much simpler form. Therefore, we will then get 2/9 which is the final answer.
Read more about it at: https://www.cuemath.com/numbers/multiplying-fractions/
Alternate Method
Interestingly, the same example with the same numbers can be solved by another simple method. Moreover, in this method, we will simplify the fractions among themselves. After doing this, we will be multiplying the numerators then, the denominators will be multiplied.
Example: Multiplication fraction of 4/12 x 16/24
Step 1. Simplify the fractions among themselves without multiplication. So, the fraction can be reduced to 1/3 x 2/3. This is the first and simple step to reduce and simplify the fraction.plication. So, the fraction can be now reduced to 1/3 x 2/3. This is the first and simple step to reduce and simplify the fraction.
Step 2. Simplify the numerator. 1 x 2= 2
Step 3. The denominators would need to be simplified. In fact, the denominator cannot be simplified prior to the numerators. Unfortunately, doing so will just cause a mess to the fraction and the result will be wrong. The denominators are, 3 x 3 = 9.
Step 4. Therefore, the final answer by solving the fraction we get is 2/9.

Fractions with Mixed Numbers Multiplication
Mixed fractions are quite different to solve as compared to other variants. Moreover, mixed fractions consist of a whole number and a proper fraction. In fact, the fraction needs to be converted with the whole number by multiplication. 23/4 is a mixed fraction, where 2 is a whole number and ¾ is a proper fraction.
Firstly, to multiply the mixed fraction, we need to change the mixed fraction into a simple fraction. Now, for example, if the mixed fraction is 22/3, we can change that into 8/3. An example is given below for a better understanding.ge the mixed fraction into a simple fraction. Now, for example, if the mixed fraction is 22/3, we can change that into 8/3. An example is given below for a better understanding.
Example: Fraction multiplication of 22/3 and 31/4
- The first step in this mixed fraction will be to convert it into a simple fraction. The whole number 2 will be multiplied by the denominator 3 which will result in 6. Moreover, after this, result 6 will need to be added by the numerator 2 that is 6+2=8. So, the answer to the first problem will be 8/3 x 13/4.
2. Now, the numerators of the improper fractions will be multiplied followed by denominators. The final result after that will come as 104/12.
3. Now, simply convert the fraction to a much simpler form by dividing the denominator with the numerator. Here, that is possible and the answer will be 26/3.
4. Interestingly, the final answer can again be converted back to a mixed fraction. So, doing that the final result will be 82/3.
This is how multiplication with mixed fractions is done. Additionally, there are other ways and techniques to do it but, this is the best and simple way.
Read more about it at: https://www.storyofmathematics.com/multiplying-mixed-numbers

Improper Fractions of Multiplication
We have learned two types of fractions and how to multiply with them. Moreover, even fractions with different denominators are very easy to multiply. But, multiplying improper fractions can be a little tricky. This is where the fractions need to be simplified and again bring the result back to mixed fractions.
Moreover, when there are two improper fractions to multiply, we frequently end up with an improper fraction. Let’s take an example with two improper fraction multiplication.
Example: 3/2 x 7/5
Step 1: Firstly, the numerators will need to be multiplied and followed by the denominators. So, (3 x 7)/ (2 x 5) = 21/10
Step 2: Interestingly, the result of solving the above question leads to an improper fraction. In fact, this improper fraction cannot be reduced into a much simpler form.
Step 3: Therefore, the final answer to the above question is 21/10 which can be changed into a mixed fraction. The result will then be, 21/10.
Improper fractions can be tricky sometimes but, if the base knowledge is correct then that might not happen. Additionally, we have discussed all the forms of fractions with multiplications. Above were the basic terms for conducting multiplications with fractions.
Read more about it at: https://www.ducksters.com/kidsmath/fractions_multiplying_dividing.php
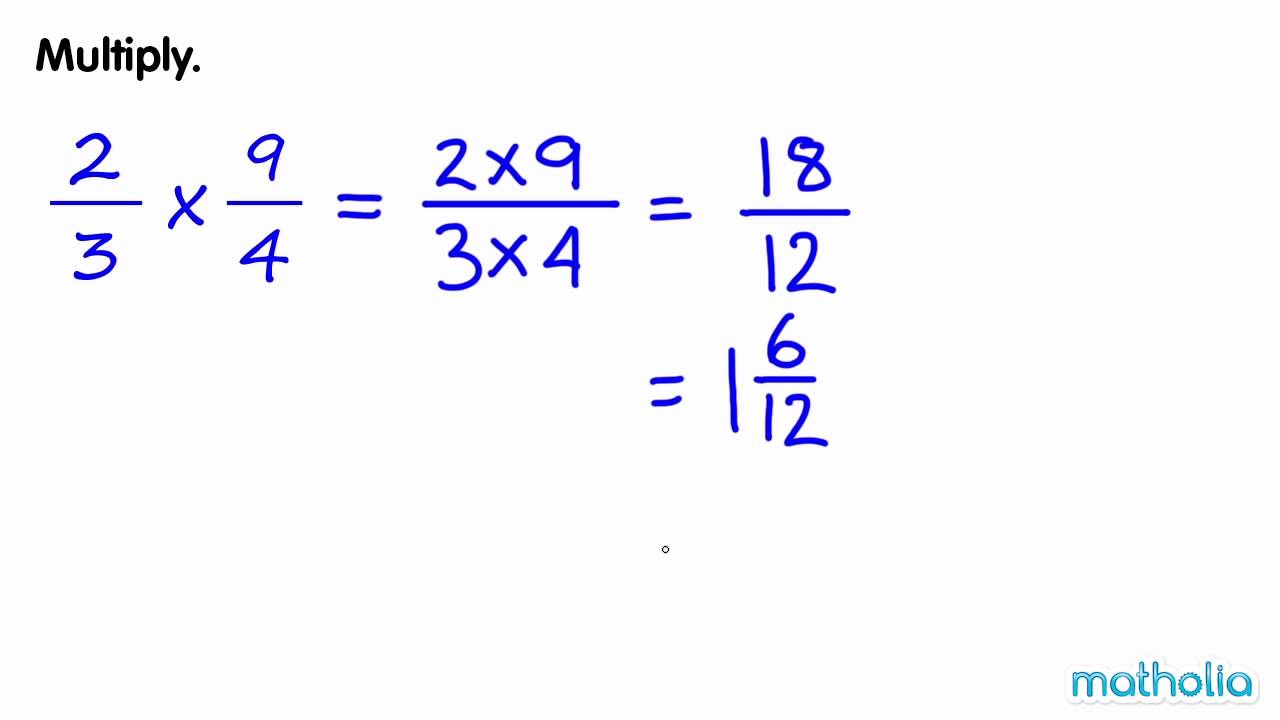
Dividing Fractions
The Division is one of the important operations under the four mathematical operations. In fact, division more or less works quite the same as subtraction. Moreover, the primary aim for division is to split the large groups into equal smaller groups.
In fact, the division is a primary arithmetic operation where various numbers are combined and divided. Now, these numbers are combined in such a way that it forms a new number. The same way division is used very often when it comes to fractions.
Division in Fractions
The base formula of division remains the same but, slightly changes when done in fractions. In fact, dividing two fractions is the same as multiplying the first by reciprocal and the second by fraction. Moreover, the first step of dividing fractions is just to find the reciprocal of the second fraction.
The next simple step to follow is to multiply the two numerators followed by the denominators. Finally, one can simplify the fraction if needed, or else the answer will remain as it is.
The example for fraction division is given below:
5/8 ÷ 15/16
1: Firstly, we will substitute the value of the numerators then followed by the denominators.
2: The result after substituting will become: 5/8 ÷ 15/16 = 5/8 x 16/15 = 2/3.
3: Now, if we simplify the above answer then the final answer would turn to 5/8 ÷ 15/16 = 2/3.
This is the basic concept for conducting fractions using division operations in mathematics. Now, we will be talking about how to simplify fractions with whole numbers.
Division with Whole Number Fractions
The Division of fractions is quite different when they are compared to multiplication. Now, division with whole numbers is quite the same process as multiplication. Firstly, we need to multiply the denominator here of the fraction with the whole number.
In fact, the first step with the whole number will be the same as with multiplication. Still, let us take an example for the following:
2/3 ÷ 4 = 2/3 x1/4
= 1/6
Now, the third step after this step would just be to simplify the result. Therefore, for the above answer, we get 1/6 as the final answer.

Dividing Fractions with Decimals
Before moving any forward we must know what is decimal. Decimal is a subpart of algebra which is another branch in Mathematics. It can be defined as a number whose whole number part and the fractional part are separated by a point. Now, this separation part of the number is called decimal.
Moreover, the dot that we put in between the numbers is called the decimal point. In fact, the digits following after the dot showcases the value smaller than one.
Now, decimal numbers are a fraction to base 10. In most cases, we can represent the decimal in the fractional form and then divide them. There are two simple steps to divide fractions with decimals and they are given below:
- Firstly, convert the given decimal to a fraction to make it look easier.
- Secondly, and lastly divide both the fractions using the simple method.
Now, if we take the example of, 4/5 ÷ 0.5. Here, we can see 0.5 as the decimal that needs to be divided in the fraction. Interestingly, the 0.5 here can be converted to 5/10 or 1/2. Moreover, now the division in fraction can be done very easily.
So, the simplified question would now be 4/5 by 1/2. Further simplifying the problem would turn into 4/5 ÷ 1/2 = 4/5 x 2/1 = 8/5. This is how decimals can be changed into a fraction and then divided with the other numbers.
Read more about it at: https://www.dummies.com/article/academics-the-arts/math/basic-math/how-to-divide-decimals-149586
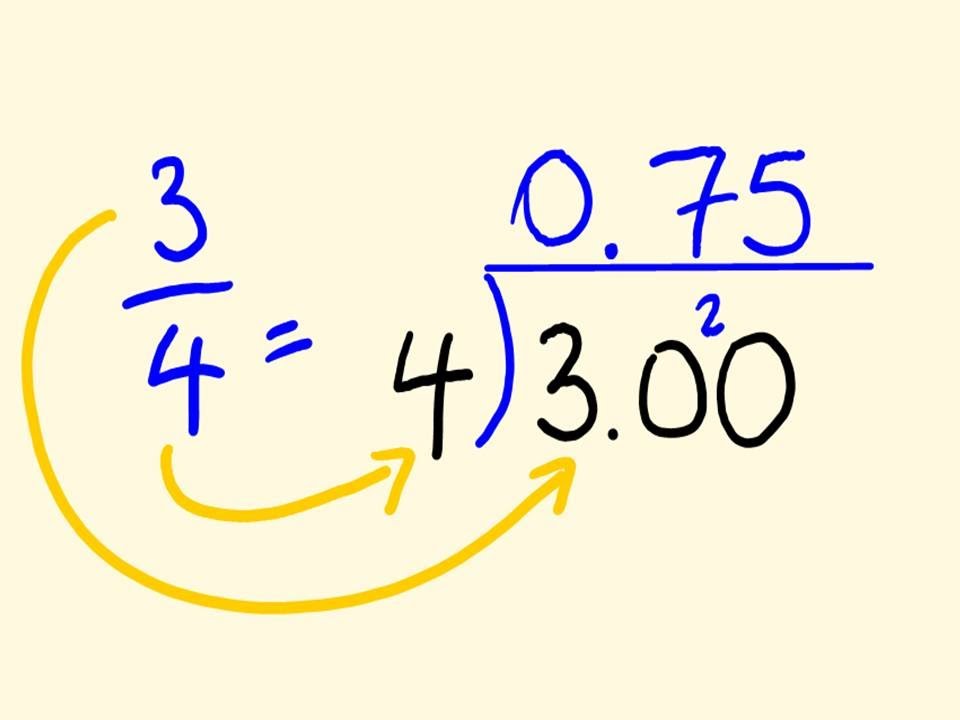
Two Ways of Dividing Fractions
There are three-four ways of dividing fractions but, we will talk about the highly used ones. In fact, the first method of dividing fractions is given above. The next two methods are given below:-https://learn.podium.school/downloads/division-with-unit-fractions-fractions-3/
Method 1: Cross-Multiplication
Step 1: This method of dividing the fraction is quite simple. Firstly, it consists of multiplying the numerator of the first fraction with the denominator of the second. This will get you a result that needs to be written down in the resulting fraction’s numerator.
Step 2: Secondly, we will then multiply the denominator of the first fraction with the numerator of the second. Again, we will need to write the answer in the resulting fraction’s denominator.
Step 3: Thirdly, after we get an answer for both sides just simplify it if possible.
![Cross Multiplying Fractions [Video & Practice Questions]](https://www.mometrix.com/academy/wp-content/uploads/2021/09/116-Cross-Multiplying-Fractions.png)
Now, let us take an example for such a case.
Example: 3/4: 6/10
The first step here would be to multiply the first fraction 3 with the denominator of the second 10. Now, doing that will give us the following fraction: 3 x 10 = 30. This answer will be written in the resulting fraction’s numerator.
Secondly, we have to multiply the denominator of the first fraction 4 with the numerator of the second 6. Now, doing that will result in 4 x 6 = 24. This answer will be written in the resulting fraction’s denominator.
Thirdly, the last step will be to simplify the fraction. Since both the numbers are divisible by 6, so we can simply divide the numerator and denominator by 6. Now, doing that will result in 30 ÷ 6 = 5 and 24 ÷ 6 =.
Moreover, the final result or the answer to the question would be 5/4.
Method 2: Inverting and Multiplying
This is another great way to solve fractions with division. In fact, we could say that it is a cross-multiplication process but, with a slight change. Let us look at the steps to divide in fractions using this method.
Step 1: The second fraction of the question must be inverted. In simple, you just need to swap the numerator for the denominator.
Step 2: Secondly, you just need to simplify the numerator with any denominator given in the question.
Step 3: Thirdly, and lastly, the interesting part is to multiply them across. This will then get you a different result and if possible just simplify that.
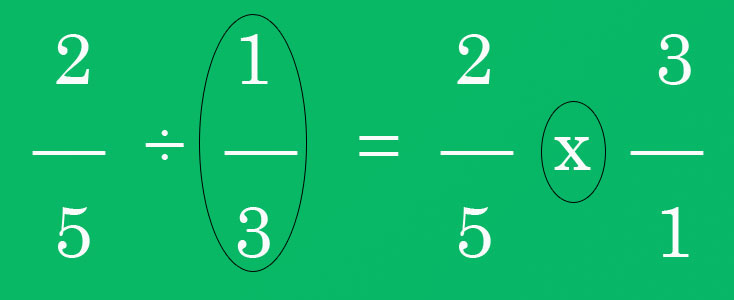
An example for such a method is given below:-
Example: 12/6: 6/4
1: As we have mentioned earlier that we need to invert the second fraction in the question. So, 6/4 will be 4/6.
2: Secondly, the numerators in the question will need to be simplified with the denominators. So, the numerators are:
12 = 2 x 2 x 3
4 =2 x 2
Denominators are:
5 = 5
6 = 2 x 3
Now, we can just simplify the numbers if they come out in common or divisible by any number. Doing this process will make the division method quite easy.
Frequently Asked Questions
- What are the basic rules for multiplying fractions?
Answer- Moreover, there are two simple rules when it comes to multiplying fractions. The first rule is to multiply numerators, and then the denominators. Now, the second rule is to simplify the obtained fraction and get the final answer.
- Why there is a need for multiplication in fraction?
Answer- A fraction is multiplied because it can break into smaller parts to make it simpler. In fact, these smaller parts can be chosen.
- What is multiplication for kids?
Answer- Multiplication is nothing but taking one number and then adding it together with a number of times.
Conclusion
After some of the intriguing concept accompanied with wonderful tips and tricks, you might be curious much to explore more. Right? So, for more information, do not forget to visit our Blog site.
Share with your friends