Math may be a difficult topic to learn for some pupils, especially if they are unaware of the greatest Vedic Maths methods. Do you know what Vedic Maths is? Vedic Maths is a gift to the globe from India’s ancient scholars. It derives its name from the Sanskrit term ‘Veda,’ which means ‘Knowledge’. It is a set of approaches or maths tricks for solving arithmetic problems quickly and easily. Furthermore, because Vedic Mathematics is so simple, computations may be performed mentally. Here, we have listed 8 Vedic Maths tricks that can help you answer your math problems with more precision and in less time. The significance of these tricks is particularly evident in exams when time is limited and questions are numerous, such as SSC, JEE, Banking Exams, and so on.

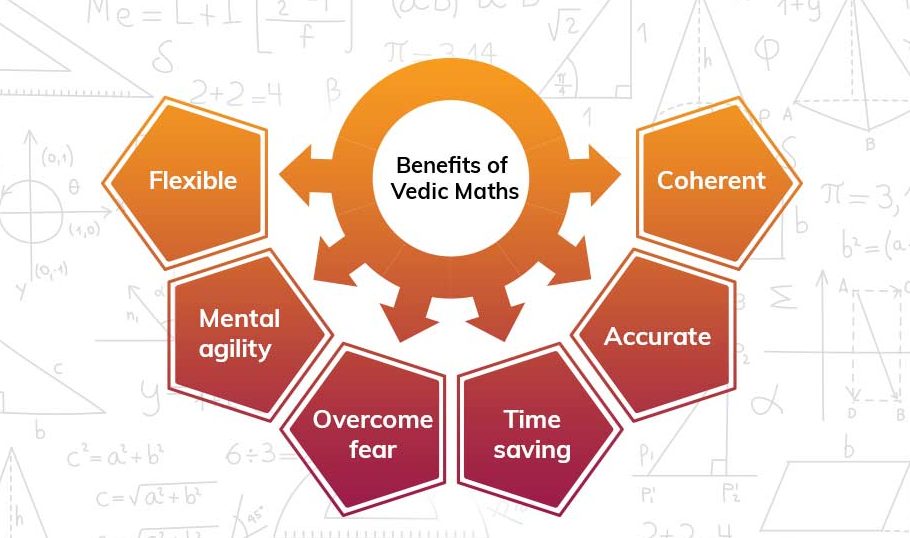
Before we look at the math tricks, let’s learn about the importance and some benefits of Vedic Maths. The image below showcases the benefits.
8 of the Best Vedic Maths Tricks
Squaring A Number With 5 as the Unit Digit
To square a number ending in 5 using Vedic Maths, multiply the digits preceding 5 by the following number. To get the solution, add 25 to the end of this number.
For example:
Find (25) ² =
Step 1: 25 x 25 = . . 25 (last 2 digits)
Step 2: 2 x 3 = 6
So, the answer is 625.
Multiply a Number By 5
It is quite simple to remember 5 tables. However, when the smaller numbers increase in size, the computation becomes more complicated. This maths trick will assist you in resolving this issue.
For example:
Even Number
1464 x 5 =
Step 1: 1464 / 2 = 732
Step 2: Then, add 0 at the end
The answer will be 2464 x 5 = 7320
Odd Number
2775 x 5
Step 1: (2775 – 1) / 2 = 1387
Step 2: As it is an odd number, instead of 0 add a 5 at the end.
So, the answer will be 3775 x 5 = 13875
Subtraction From 1000, 10000 or 100000
This is one of the simplest Vedic Maths Tricks available. All you need is one formula: subtract all digits from 9 and the last digit from 10.
For example:
1000 – 364 =
Step 1: 9 – 3 = 6, 9 – 6 = 3, 10 – 4 = 6
Step 2: Write the resulting numbers in sequence
So, the answer is of 1000 – 364 = 636
Multiplication Of Any 2-digit Number between 11 and 19
This math trick is notably useful if you cannot remember multiplication tables after 10. First, add the unit digit of the smaller number to the larger number. Then, multiply the result by 10. Now, multiply the unit digits of both the 2-digit numbers. Finally, add both the numbers.
For example:
Multiply 14 and 17.
Step 1: 17 + 4 = 21.
Step 2: 21 x 10 = 210.
Step 3: 4 x 7 = 28
Step 4. Add the two numbers, 210 + 28 and the answer is 238.
So, 14 x 17 is 238
Dividing A Large Number By 5
This maths trick will help you divide any number by 5. It consists of 2 simple steps. The first is multiplication by two, and the second is moving the decimal to the left and eliminating all the digits following the decimal point.
For example:
Divide 345 by 5
Step 1: 345 x 2 = 690
Step 2: Move the decimal: 69.0 or just 69
Therefore, the answer of 345 / 5 is 69.
Multiply Any Two-digit Number By 11
Use this maths trick to multiply a number by 11 in just 2 seconds. The key is to imagine a gap between the two digits.
For example:
Multiply 43 and 11
Step 1: 43 x 11 = 4 __ 3
Step 2: 4 (4+3) 3
So, the answer is: 43 x 11 = 473
Multiplication Of Any 3-digit Numbers
Multiplication of two 3-digit numbers using Vedic Mathematics consists of steps, which we will explain with an example.
For example:
Multiply 205 and 208
Step 1: Subtract the unit place from the number.
205 – 5 = 200
Step 2: Then, select any (1st or 2nd) number and add the unit digit of the other number
208 + 5 = 213
Step 3: Multiply the product you got in step 2 and step 1.
213 x 200 = 42600
Step 4: Then, multiply the unit digits of both. The product of these 2 numbers: 5×8=40
Step 5: Finally, add the products in step 3, and step 4
42600 + 40 = 42640
So, the final answer 205 x 208 = 63940
Find The Square Value
Calculating squares can be fairly simple if you use Vedic Mathematics.
First, select a base that is closer to the number whose square is to be discovered. Determine the number’s deviation from its base. Then, combine the difference and the n and divide the result by the base. Finally, multiply the product of the square of the difference by the result of the previous point.
For example:
(93) ² =?
Step 1: Choose 100 as base
Step 2: Then, subtract 93 from 100, which is equal to (-7)
Step 3: Add the number with the difference that you got in Step 2 = 93 + (-7) = 86
Step 4: Then, multiplying result with base = 86 x 100 = 8600
Step 5: Finally, add result with the square of the difference= 8600 + (-7)² = 8649
So, (93) ² = 8649
Final Thoughts on Vedic Maths Tricks

So, there you have it: the 8 Best Vedic Maths Tricks with Examples. These tricks are the most effective strategy to improve your exam performance. With them, you will be able to solve the majority of difficult questions in no time. Although these tricks may appear difficult at first, with continuous practice, you will be able to utilize them in no time. Therefore, we have identified some books to help you practice. They are mentioned in the video linked below.
For more content on Vedic Maths, visit the Podium School Blog.
Share with your friends