The basic equation to represent and solve an unknown quantity is the linear equation in one variable. It is easy to visualize and always follows a straight line. A linear equation is a simple way to represent a math statement. Any symbol or variable can represent unknown quantities, but the variable x generally represents the unknown quantity within the linear equation. All you need is a set of simple methods to solve a linear equation. Hence, to get the final value of an unknown quantity, the variables and constants separate from each other.
- What is Linear Equation in a Single Variable?
- Solving Linear Equation with One Variable
- Linear Equation in a Single Variable vs. Non-Linear Equations
- Applications
- Use of Linear Equations in Real Life
- Linear Equations for Word Problems
- Take a look at the problem again
- Standard Form of Linear Equations
- What is the Standard Form for Linear Equations (SFL)?
- Linear Equation Solutions
- What are the solutions to a linear equation?
- Different types of solutions for linear equations
- How do you find the solution to a linear equation?
- FAQ

What is Linear Equation in a Single Variable?
Let us quickly review linear equations before we get into the details of a linear equation in one variable. A linear equation is an equation in which each variable has the same degree. It appears as a straight line horizontally or vertically when you draw it on the graphs.
A linear equation in one variable is in the form of ax+b=0.
Here, a and b can be any integer, and x an unknown variable with only one solution.
For example: “4 plus a number gives 10”. Find the number.
You can simply say, x +4 = 10, find x. This allows us to write larger problems in a much shorter time. This equation only has one variable, x. The highest power of x in this equation is 1. These varieties of equations are linear equations with one variable because the degree of variable x is one.
Solving Linear Equation with One Variable
The general form for a linear equation is Ax+B = 0. Here, A is the coefficient for x, x is the variable, and B is the constant. The coefficient and constant term are separated from each other to solve it.
Let’s now look at how we can solve a linear one-variable equation. An equation can be compared to a weighing scale with equal weights on each side.
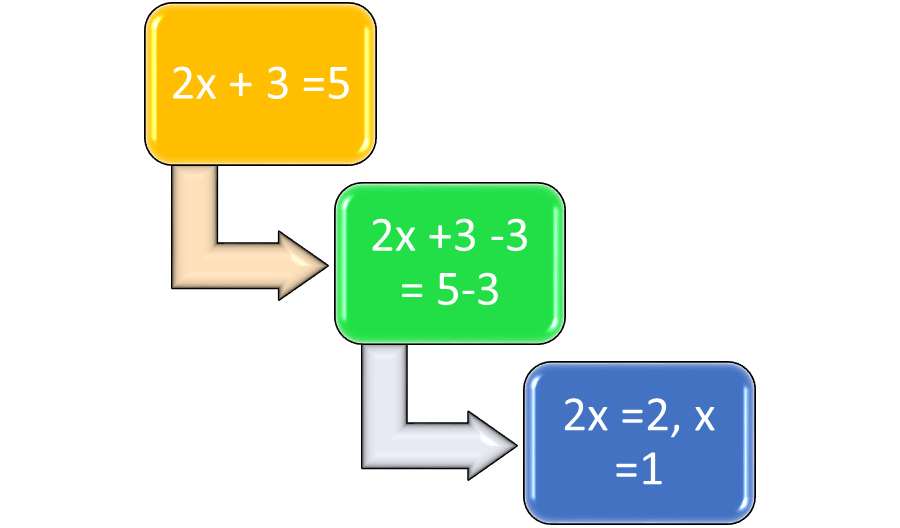
It holds the same even if we subtract or add and multiply or divide the same number to both sides of an equation.
For example: Take the following equation: 3x-2=4. So that the balance does not hamper, we will use mathematical operations to calculate the LHS and RHS. To reduce the LHS to three times, let’s add two on each side. Then, it will not affect the balance at all.
Therefore, The new LHS is now 3x-2+2=3x, and the RHS is now 4+2=6. Therefore, Let’s now divide each side by 3, to reduce the LHS down to x. So, 3x/3=6/3. Therefore, x = 2.
These points summarize the steps required to solve linear equations for one variable.
- Firstly, add or subtract both sides to keep the variable term and constants the same.
- Then, Simplify constant terms.
- Afterwards, isolate one side of the variable by multiplying or dividing it into the equation into both sides.
- Finally, simplify the answer.
Linear Equation in a Single Variable vs. Non-Linear Equations
Linear equations for one variable are single-degree equations. These are represented by a line on a coordinate plane. Non-linear equations, on the other hand, are curves or non-linear representations on the coordinate axis. Non-linear equations are generally of a higher degree. A few examples of nonlinear equations include the equation of curves, such as the circle and parabola. Ellipse and hyperbola are a few examples.
- Additionally, some examples of linear equations include x = 5, 3x+7 = 9, 4x+2y = 11. For instance: Ellipse (x2/9 +y2/16=1), equation of a circle – (x2 + y2= 25) and equation of a hyperbola (x2 /16-y2/25 =1).
It is important to note that these points will help us to summarize the concepts involved with linear equations within one variable.
- Linear equations should have a degree that is one.
- Secondly, A graph of a linear equation with one variable is a straight line, horizontally or vertically.
- A linear equation is solved in one variable will remain unchanged, regardless of any addition, subtraction or multiplication on either side.
Applications
People use linear equations every day, even without the need for a line graph, because they might face situations that have an unknown quantity. At last, this can be used to calculate mileage rates or income over time. It is important to note that the four major arithmetic operations, addition, subtraction, and multiplication, are all essential. This article will indeed explain how you can apply linear equations in real-life situations as well.
What is the Application Of Linear Equations?
The primary purpose of linear equations is to solve problems using two variables, where one variable is known and the second is unknown. This is also dependent on the previous. Meanwhile, have a look at some examples of linear equations:
- Two variables can solve geometry problems
- Then, the two variables can solve your money problems
- Two variables can solve a combination of problems.
- Also, two variables can be used to solve distance-rate-time problems
- Finally, linear equations in economics and business.
Definition of Linear Equations
A linear equation is an equation that has degree 1. A linear equation is one that you write for two variables. The equation can contain a constant, or a combination of both variables. Both are equally important. The standard form of the equation is ax+by = c. Here a and B are coefficients. X and Y are variables and c is constant. You can plot a linear equation on a graph if it is a straight line.
Use of Linear Equations in Real Life
Linear equations are something that we use almost daily in our lives, even though it means that we have to do mental calculations at times. This is the first use of a linear equation. One example of a real-life application of linear equations is to calculate the cost of hiring taxis on vacation. You can also use it to compare different rates of payment for work, budgeting, or make any predictions. Let’s take a look at an example to better understand the concept. Let’s look at the electricity used on days 1, 2, 3, and 4. The average daily amount of electricity consumed is 23 units. The average electricity consumption at the end of a day is 23 units.

For example, Let’s say we rent a car for $200 and $25 per hour. This equation is based on the fact that you don’t know how long you’ll travel. You can use “t” as the number of hours and “x” as the taxi cost.
Linear Equations for Word Problems
The use of linear equations to solve word or story problems can be challenging at first but will become easy once you understand the process. Finally, this is how it works:
Take a look at the problem again
To understand the problem, its application to a linear system, and the solution, you first carefully read it. It may be necessary to read the problem several times as well.
It is crucial that you fully understand and identify the information you are being asked for. Meanwhile, you should be aware that sometimes one word can change the way a linear system works.
Assign Variables
Use a variable to represent one of the unknown quantities/values. Then, use diagrams, tables, and other means to link all the unknown values to this variable. Write down the meaning of each variable.
Write Equations
Formulate equations that link unknown quantities to known quantities. Some of the formulas are known and can likewise be used. You can use the figure/equations from the previous step to determine which equation then leads to the answer we need.
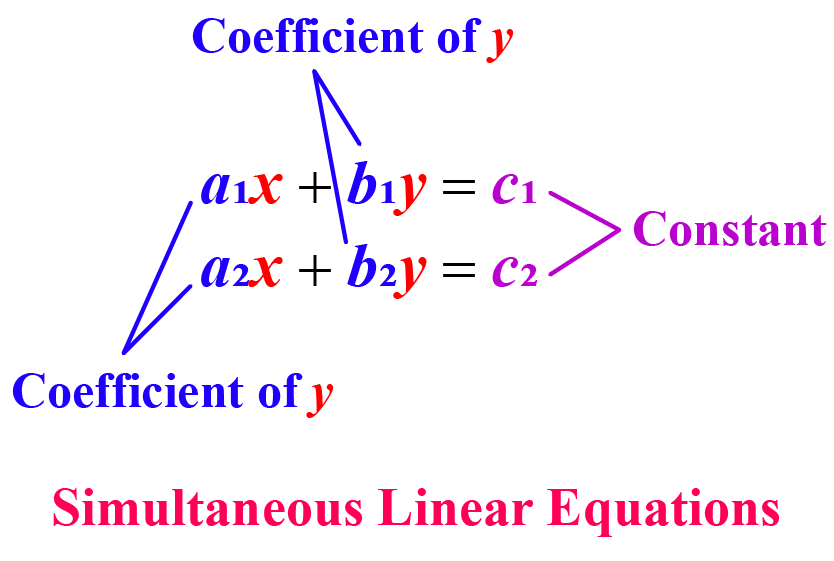
Solve the System of Equations
Answer all questions and solve the equations from the previous step. We may be asked multiple values, but only one value in the equation.
Find out the answers
It is possible to check the answer by entering it into the equation, but you must also verify that it makes sense. Recognizing that the answer is not correct can help you identify mistakes as well.
You can then solve some words by using a standard formula.
- Distance = Rate x Time
- Work Done = Work Rate x Time Spent Working
- The amount of secondary liquid in water = Percentage and Volume of Solution
Standard Form of Linear Equations
A method for writing linear equations is the standard form of linear equations. Three forms of linear equation: the standard, slope-intercept, and point-slope. The general form of linear equations, which refers to Ax + B = C, is also the standard form. Ax + B = C is its general representation.
What is the Standard Form for Linear Equations (SFL)?
A linear equation is an equation, where the highest power of the
variable = 1 or a one-degree equation. A linear equation is 4x + 6 = 6. The most common form of a linear equation is Ax + B = C. Here, integers are A, C, and B, and the variables are x and y.
Standard Form of Linear Equations with One Variable
- A linear equation with one variable is an equation that has one variable. It means that the linear equation only has one solution. The standard or general form of linear equations within one variable.
Standard Form of Linear Equations with Two Variables
Two solutions are possible for a linear equation that has two variables. This is the standard form of linear equations or general form of linear equations in two variables.
Ax + by = C
- Where A, C, and B are integers
- The variables x and y are referred to as
- For example, the standard form for a linear equation with two variables is 3x + 4y = 8.
How do you write the Standard Form of Linear Equations with Two Variables?
If we need to change the standard form of a linear equation, we can then convert it easily in the general form. Axe + B = C where A, B, and C should all be integers, and the terms in the order given.
For example: Write the linear equation in standard form. 2y = 5x + 7
Solution To rewrite the equation in standard form we will transpose -5x to the left-hand side. It will now be 2y + 5x = 7. We can now arrange the terms as per the standard form. It will be 5x + 2y = 7. This equation is in its default form.
Linear Equation Solutions
Linear Equation solution refer to all possible solutions for the variables of linear equations. They can involve unknown quantities, which one or more variables represent. It allows you to calculate the cost, distance, speed, and mileage. It is easy to use.

This lesson will cover the types of solutions and the methods to find them.
What are the solutions to a linear equation?
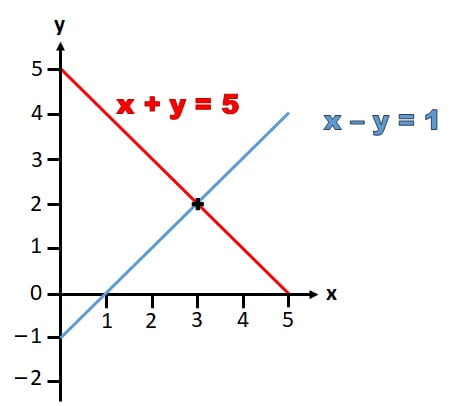
The point where the lines or planes represent linear equations intersect or meet are the solutions to linear equations. The solution set for a system with linear equations is the collection of values that correspond to all possible solutions. For example – Visualize the solution to a system’s simultaneous linear equations and solve them by drawing two linear graphs and finding their intersection point.
- The blue line is for equation 2, while the red line shows all solution to equation 1. You can find the solution to both equations at the intersection at a unique point (2.4).
Different types of solutions for linear equations
A unique solution to a system linear equations
A linear equation can only have one solution. This means that L.H.S. and R.H.S are equal at the substitution point. A linear equation is solved in one variable has a unique solution. 3m = 6 has the unique solution m = 2, for which L.H.S. = R.H.S. Similar to above, for simultaneous linear equations within two variables, the unique solution m = 2 for which L.H.S = R.H.S.
There is no solution
If there is no point at which lines intersect or if the graphs of linear formulas are parallel, linear equations cannot be solved.
Infinite Many Solutions
- If there are solutions, set of infinite points for which L.H.S. and R.H.S are equal or if the lines intersect, then a system of linear equations can have infinitely many solutions.
How do you find the solution to a linear equation?
Linear Equations Solutions in One Variable

Take the following equation into consideration: 2x + 4 = 8.
- Firstly, subtract 4 from L.H.S to find the value of. Then, subtract 4 from both ends of the equation. 2x + 4 – 4 = 8 – 4
- Simply. We now have 2x = 4.
- Then, to get x we need to subtract 2 from L.H.S. Therefore, we divide the equation by 2. 2x/2 = 4/2, x=2
Therefore, the solution to the equation 2x +4 = 8 is x=2.
Linear Equations with Two Variables: Solutions
These methods are useful for solving linear equations involving two variables.
Substitution Method
Let’s look at the following pair linear equations.
x +y = 4, and x-y = 2.
- Let’s change the first equation so that y can be expressed in terms of x.
- This expression can be used to substitute for y in the second equation. We will now have an equation in x only: x-y = 2, 4+ x= 2, 2x= 6, x= 6 x= 6/2, and x= 3
- Once we have the value for x, we can use it to plug it into the other equations to get y. Let’s put it in the first equation: x+y = 4 (3) +y = 4, y= 4 – 3 = 1, and y= 1
- The last non-trivial solution to this problem is: x = 3 and y = 1.
This is why substitution is used. One variable can be expressed in terms of another by using one of the equations, and the expression is then substituted into the second equation.

Elimination Method
Take a look at the following pair of linear equations.
2x + 3y – 11 = 0, 3x + 2y – 9 = 0
These equations have x coefficients of 2 and 3. Firstly, let’s multiply the first equation by 3 and the second by 2, to equalize the coefficients of the x in both equations.
- 3 2x + 3y – 11 = 0 6x + 9y – 33 = 0
- 2 3x + 2y – 9 = 0 6x + 4y – 18 = 0
Let’s now subtract the equations. This means we subtract the left-hand side of each equation. The right-hand side will remain unchanged.
6x + 9y – 33 = 0 ,6x + 4y – 18 = 0 0 + 5y – 15 = 0, 5y = 15, y = 3
Notice how x is eliminated and that we have an equation in y. Once we have the value for y, we can continue as before – we simply plug it into one of the equations. Let’s put this in the first equation.
2x +3y -11 = 0, 2x+3 (3) -11 = 0, 2x+9 -11 = 0, 2x+9 -11 = 0, 2x+9 -11 = 0, 2x+9 –11 = 0, 2x+9 -11 = 0, 2x+9 -11 = 0. 2x = 2, 1x = 1.
The non-trivial solution to this problem is: x = 1, and y = 3.
Graphical Method
Let’s take the following example: x – y + 2 = 0, x + y = 5 = 0. The lines are drawn on the same axes.
(1) is the point of intersection, meaning that x = 1 and y = 3, respectively, are solutions to the pair (2) of linear equations. It is the only solution for the pair. Two non-parallel lines can’t intersect at more than one location.
Important Notes
The following conditions can be used to check the solutions available:
- Unique solution (consistent, independent) a1/a2/b1/b2
- There is no solution (inconsistent, independent) for a1/a2 =/b1/b2 c1/c2
- There are infinite solutions (consistent, dependent)
Some Best Examples
Example 1: David was a stenographer. He was paid $50 per hour in June. For the days that he was absent, $10 was deducted from his daily salary. For the number of days worked, he was paid $900 What was the number of days he worked?
Solution:
Let x be the number of workdays. Therefore, his days off work would be = 30 + x. For each day that he worked, he was paid $50 and for every day that he didn’t work, $10 was deducted. He received $900 at the end of each month. The given information allows us to form a linear equation with one variable, as 50(x)-10(30 x) =900
50x – 300 + 10x = 900
60x = 900 + 300
x = 1200/60
x= 20
David, therefore, worked for 20 consecutive days.
FAQ
Question 1. What are the types of equations?
Answer = Types of equations
- linear equation for degree one.
- quadratic equation for degree two.
- cubic equation for degree three.
- quartic equation for degree four.
- quintic equation for degree five.
- sextic equation for degree six.
- septic equation for degree seven.
- octic equation for degree eight.
Question 2. What is an equation in economics?
Answer = An equation is basically a mathematical way to look at the relationship between concepts. Variables are used to represent these concepts and items. Variables are often used in Economics, but then you can also represent them by the first letter of an item.
Question 3. What are the elements of an equation?
Answer = Expressions can contain one or more of the following components: symbolic names, mathematical operators, functions, and conditional expressions.
Share with your friends