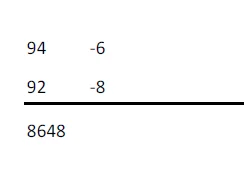- What is Vedic Mathematics?
- What are the 16 Vedic sutras?
- The 16 Sutras of Vedic Math
- One of the Sutras, for example, is titled ‘Vertically and Crosswise.’
- The History of Ancient Mathematics
- Father of Vedic History and mathematics
- Vedic maths and Human Mind
- Important features of the Vedic Mathematics Sutras
- Vedic Maths in Modern Times
- SOME QUICK FAQS FOR YOU
- Q.1 What is Vedic maths and its benefits?
- Q.2 What is the right age to learn Vedic maths?
- Q.3 Why Vedic maths should be taught in the schools?
- Q.4 How many levels are there in the Vedic maths?
- Q.5 How long does it take to learn Vedic maths?
- Q.6 Is Vedic maths difficult?
- Q.7 How do you introduce Vedic maths?
- Q.8 What is Vedic Math methods ?
- Q.9 What is Vedic maths with example ?
- Q.10 What is the difference between Maths and Vedic Maths?
- Q.11 How is Vedic maths helpful to modern maths?
- Q.12 What are the 16 formulas of Vedic maths ?
- Q.13 Who is the founder of Vedic maths?
- Q.14 What are the topics in Vedic maths?
- Final Thoughts
What is Vedic Mathematics?
Vedic Mathematics is a book which is written by a Hindu monk Sri Bharati Krsna Tirthaji (1884-1960). To simply put it out, Vedic Maths acts really helpful in solving problems related to arithmetic, algebra, conics, geometry etc easily.
What are the 16 Vedic sutras?
Vedic mathematics is described using sutras, a small collection of aphorisms. Also sutras are naturally occurring mental processes that can be used to solve mathematical problems in the simplest way possible. The sutras describe such principles and practices.
Each sutra includes a wide range of applications, as well as ways to use it. Most importantly Vedic mathematics is founded on sixteen Sutras also called formulas.
The 16 Sutras of Vedic Math
- Ekadhikina Purvena
(Corollary: Anurupyena)
Meaning: By one more than the previous one - Nikhilam Navatashcaramam Dashatah
(Corollary: Sisyate Sesasamjnah)
Meaning: All from 9 and the last from 10 - Urdhva-Tiryagbyham
(Corollary: Adyamadyenantyamantyena)
Meaning: Vertically and crosswise - Paraavartya Yojayet
(Corollary: Kevalaih Saptakam Gunyat)
Meaning: Transpose and adjust - Shunyam Saamyasamuccaye
(Corollary: Vestanam)
Meaning: When the sum is the same that sum is zero - (Anurupye) Shunyamanyat
(Corollary: Yavadunam Tavadunam)
Meaning: If one is in ratio, the other is zero - Sankalana-vyavakalanabhyam
(Corollary: Yavadunam Tavadunikritya Varga Yojayet)
Meaning: By addition and by subtraction - Puranapuranabyham
(Corollary: Antyayordashake’pi)
Meaning: By the completion or non-completion - Chalana-Kalanabyham
(Corollary: Antyayoreva)
Meaning: Differences and Similarities - Yaavadunam
(Corollary: Samuccayagunitah)
Meaning: Whatever the extent of its deficiency - Vyashtisamanstih
(Corollary: Lopanasthapanabhyam)
Meaning: Part and Whole - Shesanyankena Charamena
(Corollary: Vilokanam)
Meaning: The remainders by the last digit - Sopaantyadvayamantyam
(Corollary: Gunitasamuccayah Samuccayagunitah)
Meaning: The ultimate and twice the penultimate - Ekanyunena Purvena
(Corollary: Dhvajanka)
Meaning: By one less than the previous one - Gunitasamuchyah
(Corollary: Dwandwa Yoga)
Meaning: and the product of the sum is equal to the sum of the product - Gunakasamuchyah
(Corollary: Adyam Antyam Madhyam)
Meaning: and the factors of the sum is equal to the sum of the factors
One of the Sutras, for example, is titled ‘Vertically and Crosswise.’
Step 1
Multiply the digits at the unit place. Here they are 2 and 4 . Because the number is eight, you keep the digit in the units location. If there are two digits in a case, carry the tenth digit to the next place value.
Step 2
Multiply the digits at the unit’s place to the digit at the tenth place and add both of them. Also keep the first digit of the unit and carry the rest of the digits to the next place value. And this is an across step. When we multiply 1 by 4 and 2 by 3 in the given example, we get 4 and 6. When we added them up, we got a total of ten. We kept 0 and moved 1 to the following position.

Step 3
Multiply the tenth-place digits. To the carry over digits, add the digits. And this stage should be referred to as vertically once more. In this step, we multiplied 1 by 3 and added the carryover 1 from the previous step.
Hence the answer is 408
The History of Ancient Mathematics
In the sixth century BC, the Pythagoreans, who coined the term “mathematics” from the Greek (mathema), which means “stuff of teaching,” began studying mathematics as a “demonstrative science.”
The customs of the Greeks were significantly polished. The advent of synthesis and mathematical rigors in proofs, in particular, widened the scope of arithmetic’s subject matter.
Though they created just about no contributions to theoretical mathematics. The traditional Romans used math in measuring, structural engineering, technology, accounting, creation of satellite and star calendars, and even arts and crafts.

Chinese mathematics created early contributions, as well as an area price system and also the initial use of negative numbers. The Hindu–Arabic numeral system and also the rules for the utilization of its operations, in use throughout the globe these days evolved over the course of the primary millennium AD in Asian nation and were transmitted to the Western world via monotheism mathematics through the work of Muḥammad ibn Mūsā al-Khwārizmī.
Monotheism mathematics, in turn, developed and dilated the arithmetic renowned to those civilizations.

Father of Vedic History and mathematics
The Father of Vedic Mathematics is Shri Bharati Krishna Tirathji. He attained self-realization at Shringeri Matha under the guidance of Shri Shankracharya as well as Shri Sachidananda Shiva Abhinava Narsimha Saraswati.
From 1911 to 1918, he spent 7 years in deep meditation and Vedanta study, living as a Sadhu. During this time, the 16 Vedic Maths Sutras were written. After being inducted into Sanyas by Shri Trivikram Teerathaji of Varanasi in July 1919, he was given the name Shri Bharti Krishna Tirthaji.

In 1921, Shri Trivikram Tirathji made him the Head of Dwarikapeeth. From 1925 till his Mahasmadhi in 1960, he was the abbot of the Govardhan Math Monastry in Puri, Orissa.
Vedic maths and Human Mind
The portrayal of distinct brain zones engaged in highly active activity dealing with mathematics is at the heart of a growing neuroscientific knowledge of the mathematical functioning of human brains. As a matter of fact understanding these brain zones and how they work mathematically provides unmistakable clarity and a solid foundation for building exceptional mathematics education.
We read and communicate with others while learning or discussing mathematics, and we talk, write, and draw diagrams when communicating mathematical issues.

As a result, we can expect a close relationship between the human brain’s mathematical operations and the language in which we explain the problem. We are unable to discover a suitable solution to the incorrectly presented problem. As a result, the presence of mind and the capture of thoughts while presenting the problem are just as important as the solution to the problem.
Vedic maths formulas
The formula identifies the way our mind functions naturally and is therefore helpful in guiding the student to the correct method of solving the question.
Therefore, understand that Sutras explain the mental process that occurs when we struggle to find out the solution to given problems.

In the first place, a structure constructs where we develope formulas to solve the problems and apply them anywhere possible while not leaving the basic fundamentals aside . All of this takes place within the human mind. As a matter of fact there is no mention of using paper and pen when practicing Vedic maths.
Vedic maths was generally performed spontaneously, with a strong emphasis on improving students’ mental abilities. While reading the Vedas, we frequently come across numerous occurrences in the lives of great pupils who have been put to the test by their gurus by putting them through real-life obstacles or sending them straight into battle.
These Heroes were quoted accomplishing some astonishing things in the Mahabharata, Ramayana, and other holy literature, such as flying stones while constructing the Rama Setu bridge, Arjuna, and the bird’s eye account, and locating the directions in the wilderness with such ease. Without information, none of this would have been possible. Lower caste workers such as carpenters, craftsmen, and traders have long used these mathematical procedures for mental arithmetic. Vedic mathematics is built using these mental processes.
Important features of the Vedic Mathematics Sutras

- Perhaps the most remarkable feature of the Vedic Mathematics Sutras system is its clarity. Instead of a confusion of unrelated methods, the vedic maths system is interrelated and connecting.
Finding the square of a number in using Vedic Maths Trick is easy. Just follow the below steps:
Step 1. Take a base number closer to the original number.
Step 2. And find the difference of the original number from the base.
Step 3. likewise, add the difference with the original number.
Step 4. Multiply the result with the base.
Step 5. By the same time add the product of the square of the difference with the result of the above point.
(99) ² =?
Step 1. Lets take100 as base
Step 2. Difference will be: 99-100 = -1
Step 3. Add the number with the difference that you got in Step 2 = 99 + (-1) = 98
Step 4. Multiplying the result with base = 98*100 = 9800
Step 5. Now, add result with the square of the difference= 9800 + (-1)² = 9801
So our answer is : (99) ² = 9801

- Anyone can solve difficult problems and huge sums by using methods of Vedic maths. Certainly, these easy to remember methods are part of mathematics which is far more structured than the modern ‘system’. Vedic Mathematics demonstrate the reasonable and logical system of mathematics and not to mention the formulas are complementary, direct, and easy.
The verses are guide to turn difficult sums into quick mental maths using simple rules.
The Nikhilam Navatashcaramam Dashatah – “all from nine, last from ten”
For example, speeds the multiplication of large numbers by breaking them down to their common bases :
(1) To multiply 48 by 52, the numbersare borken into (50-2) and (50+2) and the square of the smaller sum (4) subtracted from the square of the larger (2,500) to reach the answer of 2,496.
- Above all the clarity of Vedic Mathematics helps carrying out calculations mentally. Similarly, there are various benefits of using your mind with the knowledge of all its functions. People with deep research and analysis can invent their own formulas. As their knowledge should not face any restrain of that one ‘correct’ method. As a result there will be creativity, clarity, development of interests, and useful inventions in the fields of mathmatics.
- People are taking interests in the vedic maths and shown their desire to add it into the syllabus of school children. Meanwhile, mathematics teachers are also looking for something better and finding the Vedic system is the answer.There are various researches which includes the advantages of learning Vedic Maths on children; developing new, logical and easy applications of the Vedic Sutras in geometry, calculus and computing, etc.
However, without really applying the Vedic system, it is impossible to truly appreciate the usefulness and potency of Vedic Mathematics. Only then can it be seen as the purest and most cohesive mathematical system possible.
Vedic Maths in Modern Times
Vedic mathematics aids in mental computations that are both faster and more accurate. This combines 16 Sutras and 13 up Sutras. Mental calculations are beneficial to answer any complex equation in addition, division, multiplication, algebra, trigonometry, square, square root, cube, and cube root. And this is an ever-changing epoch in the human history. UPSC, GPSC, CET, GATE, JEE, and many other competitive exams Vedic math aids in faster mental calculations and reduces the time required to solve tough mathematical problems.
How Vedic maths overcome Maths Phobia

- Firstly, the mathematical applications and benefits are secondary benefits. The first and most important benefit is that it aids in the coordination of both hemispheres of the brain. This boosts efficiency across the board.
- Secondly, vedic mathematics also aids students in overcoming their apprehensions about math and regaining their confidence. Making mathematics more approachable helps pique people’s interest in the topic. Similarly, many studies have been conducted in recent years in a variety of fields. Likewise, many universities have begun to offer courses in Vedic math, yoga, and Vedic literature, which are gaining popularity.
Vedic Maths and Space Science

The rise in popularity of vedic maths is due in part to the prime minister, Shree Narandra Modi, renewing his drive to stake India’s claim to the foundations of human knowledge. Not only he claimed that India’s ancient vedic scientists were responsible for the country’s successful trip to Mars last year but also envisioned flying travel thousands of years before the Wright Brothers flew for the first time. It had been an eventful day. A disputed ‘veda’ that depicted ancient air flight between Indian towns and to other parts of the world planets.
- Mr. Modi recently stated that Lord Ganesha, the Hindu God with the elephant head, was proof of Plastic surgery was known to early Indians. Additionally, there have also been allegations that algebra, trigonometry, and calculus are useless. Moreover, India gave us the Pythagorean theorem, the concept of zero, and the decimal system.
- It is so versatile that NASA scientists make use of some of its principles in the field of artificial intelligence. Therefore, Vedic Mathematics is now taught in schools, with extra attention given to those who are interested in learning more about the topic.
Vedic Maths help in overall Personality development of a student
- Integrity: Because of the subject’s integrity, learning becomes simple together with instant results. As a matter of fact , every sutra and upasutra are consistent and connected. Furthermore, we can use a single rule and can apply it on a number of different tasks.
- The simplicity of Vedic mathematics makes it significant. Let’s imagine you’re doing multiplication with the current popular method, which takes 3, 4, 5, or more than five steps depending on how much you multiply. However, the Vedic Calculation methodology gives you a result in one step regardless of how much you multiply. It appears to save you time and boost your productivity.
- Creativity can manifest itself in a number of ways. Meanwhile, a single inquiry or, to put it another way, a single problem can be solved using any solution. In the same way, It inspires you to go outside the box and come up with your own solution to the problem.
- Fast and Accurate Results: Most importantly we can solve many problems in one step, saving time and reducing the number of phases.
SOME QUICK FAQS FOR YOU
Q.1 What is Vedic maths and its benefits?
When compared to the traditional method and it allows for speedier calculations. In addition, It encourages mental computation. It improves students’ mathematical understanding. Furthermore,the spiritual side of a child’s personality is improved via Vedic math. Boost your inventiveness and self-assurance.
Q.2 What is the right age to learn Vedic maths?
The ideal age to study Abacus is between the ages of 5 and 14, and the best age to learn Vedic maths is between the ages of 10 and 14.
Q.3 Why Vedic maths should be taught in the schools?
Not only It helps individuals complete issues quickly , accurately but also improve their attentiveness. The boring and dry methods employed in schools to teach Math are the primary cause of indifference in the subject. And It’s not enjoyable, and teachers frequently overcomplicate it.
Q.4 How many levels are there in the Vedic maths?
There are in total 4 levels in Vedic maths.
Q.5 How long does it take to learn Vedic maths?
What is the length of time it takes to master Vedic Maths? The length of time it takes to complete the course varies depending on who is taking it, but it usually takes between 30 and 60 hours.
Q.6 Is Vedic maths difficult?
It is a set of approaches for solving arithmetic problems in a simple and efficient manner. Not only ‘Difficult’ problems or large sums can be addressed instantly using Vedic methods but also can be applied solving matters of real life . Because of its simplicity , we do all the calculations mentally.
Q.7 How do you introduce Vedic maths?
Vedic Mathematics is not a distinct branch of mathematics, but rather a part of everyday mathematics. The mathematical problems can be solved mentally or in one-two steps using 16 main Vedic equations, however the routine/conventional way takes much longer. Vedic approaches conserve time, space, and energy.
Q.8 What is Vedic Math methods ?
Vedic Mathematics is a set of techniques/sutras for quickly and easily solving mathematical problems. Equally important, It is made up of 16 Sutras (Formulae) and 13 Sub-Sutras (Sub Formulae) that can be applied to a variety of issues in arithmetic, algebra, geometry, calculus, and conics.
Q.9 What is Vedic maths with example ?
Once you practice this Vedic Trick for a number of times, you might never need a calculator to get the result as you will calculate faster than the machine. Similarly with this Vedic Math trick, you can quickly find the square of a two-digit number ending with 5.
For example Find (55) ² =?
Step 1. 55 x 55 = . . 25 (end terms)
Step 2. 5x (5+1) = 30
So our answer will be 3025.
Well, if you have understood the process try to find the square of 75 & 95.
Q.10 What is the difference between Maths and Vedic Maths?
Vedic Math differs from traditional math in that it is coherent, and rather than employing different processes for different problems, it solves them using its coherence quality. And Vedic math is simple, requiring pupils to mentally complete the steps required to solve a problem.
Q.11 How is Vedic maths helpful to modern maths?
During this time, things are constantly shifting. As a matter of fact, Vedic mathematics enables mental computations to be performed more quickly and precisely. There are 16 sutras in total, 13 of which are up sutras.
Any complicated problem in addition, division, multiplication, algebra, trigonometry, square, square root, cube, and cube root can be solved using mental calculations. Furthermore,the current epoch is the most rapidly expanding in human history.
Q.12 What are the 16 formulas of Vedic maths ?
EKADHIKENA PURVENA
(Corollary: Anurupyena)
Meaning: By one more than the previous one
• Nikhilam Navatashcaramam Dashatah
(Corollary: Sisyate Sesasamjnah)
Meaning: All from 9 and the last from 10
• Urdhva-Tiryagbyham
(Corollary: Adyamadyenantyamantyena)
Meaning: Vertically and crosswise
• Paraavartya Yojayet
(Corollary: Kevalaih Saptakam Gunyat)
Meaning: Transpose and adjust
• Shunyam Saamyasamuccaye
(Corollary: Vestanam)
Meaning: When the sum is the same that sum is zero
• (Anurupye) Shunyamanyat
(Corollary: Yavadunam Tavadunam)
Meaning: If one is in ratio, the other is zero
• Sankalana-vyavakalanabhyam
(Corollary: Yavadunam Tavadunikritya Varga Yojayet)
Meaning: By addition and by subtraction
• Puranapuranabyham
(Corollary: Antyayordashake’pi)
Meaning: By the completion or non-completion
• Chalana-Kalanabyham
(Corollary: Antyayoreva)
Meaning: Differences and Similarities
• Yaavadunam
(Corollary: Samuccayagunitah)
Meaning: Whatever the extent of its deficiency
• Vyashtisamanstih
(Corollary: Lopanasthapanabhyam)
Meaning: Part and Whole
• Shesanyankena Charamena
(Corollary: Vilokanam)
Meaning: The remainders by the last digit
• Sopaantyadvayamantyam
(Corollary: Gunitasamuccayah Samuccayagunitah)
Meaning: The ultimate and twice the penultimate
• Ekanyunena Purvena
(Corollary: Dhvajanka)
Meaning: By one less than the previous one
• Gunitasamuchyah
(Corollary: Dwandwa Yoga)
Meaning: and the product of the sum is equal to the sum of the product
• Gunakasamuchyah
(Corollary: Adyam Antyam Madhyam)
Meaning: The factors of the sum is equal to the sum of the factors.
Q.13 Who is the founder of Vedic maths?
Bharati Krishna Tirtha, an Indian monk, wrote Vedic Mathematics, which was originally published in 1965.
Q.14 What are the topics in Vedic maths?
In Vedic Maths, there are 16 sutras. These sutras are frequently referred to as Vedic Maths techniques or quick computation procedures.
Final Thoughts
Vedic Mathematics is one of the most natural ways of working and can be learnt with very little efforts. Vedic Mathematics is also supported by a set of checking procedures. The calculation techniques provided are highly creative as well as effective. Additionally, Vedic Mathematics continues to be the center of attention and researches are spanning across the globe. And many students are resorting to the use of Vedic Maths; especially the ones who sought to appear for competitive exams. Furthermore, Vedic mathematics offer students the extra edge that general mathematics might not be able to provide them with.
These days, Vedic Mathematics is being taught at school level and special attention is being provided to student those who want to learn more about the subject.
Share with your friends