How to multiply using the Urdhva Tiryagbyham technique?

Urdhva Tiryagbyham is a shortcut method/ Sutra 3 for the multiplication of all types of numbers in Vedic Mathematics. The English translation for the same is Vertically and Cross-wise. For numbers up to 3 digits, we can easily use the normal process of this method. Yet for numbers having more than 3 digits, the Vinculum process is used to convert the negative numbers into normal numbers.

Let us start by learning one method at a time.

Shortcut method for multiplication of 2 numbers.

We will follow this procedure from the left to the right.

Let us take two numbers- 22 and 24

The steps:

1. First, we will multiply the first digits of both numbers. Therefore we will multiply 2*2 which will give us 4. Write it separately.
2. Then cross-multiply both digits of both numbers. That is we will multiply 2*4 which will give us 8 and 2*2 which will give us 4.
3. Add both these numbers (8+4). The answer is 12.
4. The last step is to multiply the last digits of both the numbers i.e 2*4 which gives us 8.
5. For our final answer, we will place the digits according to their place value i.e 8 in the unit’s place. Also as we have a double-digit number in our tens place i.e 12 we will carry forward the 1 and add it to the number which is placed in the hundreds place (1 will be carry forwarded and added to 4 which we had written separately in Step 1.-1+4=5(in the hundreds place)
6. Therefore, our final answer is 528.

Let us try with another example:

Let us take two numbers- 43 and 54

The steps:

1. First, we will multiply the first digits of both numbers. Therefore we will multiply 4*5 which will give us 20. Write it separately.
2. Then cross-multiply both digits of both numbers. That is, we will multiply 4*4 which will give us 16, and 3*5 which will give us 15.
3. Add both these numbers (15+16). The answer is 31.
4. The last step is to multiply the last digits of both the numbers i.e 3*4 which is equal to 12.
5. For our final answer, we will place the digits according to their place value i.e 2(from 3*4=12) in the unit’s place. For the ten’s place, we already have the number 31 but 1 from the above 12 will be carry forwarded and added to 31 and therefore we have 32.

Now from 32, we will leave 2 in the tens place and 3 will be carry forwarded and added to the 20 that we wrote separately in the 1^st step giving us 23.

• Therefore, finally appending all the digits our final answer is 2322.

Shortcut method for multiplication of 3-digit numbers.

 We will follow this procedure from the left to the right

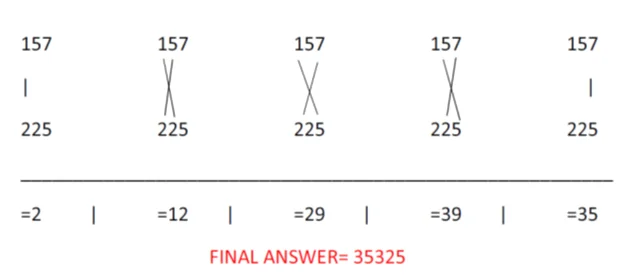
• Let us take 2 numbers – 157 and 225
• Here the cross multiplications are a little tricky therefore make sure to concentrate.
• First, we will simply multiply the 1^st digits of both the numbers i.e 1*2 which gives us 2.
• Then we will cross multiply the 1^st two digits of both numbers and add their answers. Therefore, (1*2) +(2*5) = 12 is our answers. Make sure to write these numbers separately so that you don’t mix them up while finding out the final answer.
• Then, we will cross multiply the first and last digits of both numbers and vertically multiply the center digits of the same and add all three of them together. Therefore, <(1*5)+(5*2)+(7*2)>=29 is our answer for this equation.
• Again, we will cross multiply the 2^nd and 3^rd digits of the numbers. (5*5)+(7*2)>= 39
• For the final equation, we will have to multiply the last digits of the numbers vertically. Therefore, our last equation summarizes to (7*5)= 35.
• We have answers from all the equations. Lets’ write them down – 2,12,29,39,35.
• To solve this we will use the carry forward method.
• Doing this, our final answer will come out to be as 35325.

Urdhva Tiryagbyham – One more Example

We will follow this procedure from the left to the right

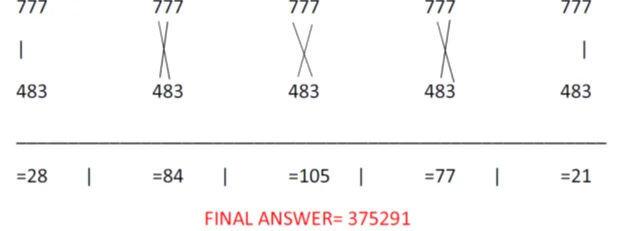
• Let us take 2 numbers – 777 and 483
• Here the cross multiplications are a little tricky therefore make sure to concentrate.
• First, we will simply multiply the 1^st digits of both the numbers i.e (7*4) which gives us 28.
• Then we will cross multiply the 1^st two digits of both numbers and add their answers. Therefore, (7*8) +(7*4) = 84 is our answer. Make sure to write these numbers separately so that you don’t mix them up while finding out the final answer.
• Then, we will cross multiply the first and last digits of both numbers and vertically multiply the center digits of the same and add all three of them together. Therefore, (7*3)+(7*8)+(7*4)=105 is our answer for this equation.
• Again, we will cross multiply the 2^nd and 3^rd digits of the numbers. (7*3)+(7*8)= 77
• For the final equation, we will have to multiply the last digits of the numbers vertically. Therefore, our last equation summarizes to (7*3)= 21.
• We have answers from all the equations. Lets’ write them down – 28,84,105,77,21
• To solve this we will use the carry forward method.
• Doing this, our final answer will come out to be as 375291.

• Shortcut method for multiplication of 4-digit numbers.

 We will follow this procedure from the left to the right

• Let us take two numbers – 2345 and 3456
• We will start with vertical multiplication of 1^st two digits of the numbers(2*3)
• Then we will crosswise multiply and add 1^st 2 digits of both numbers <(3*4)+(3*3)>
• Crosswise multiply and add 1^st 3 digits of both numbers <(2*5)+(3*4)+(4*3)>
• Crosswise multiply and add all the digits <(2*6)+(3*5)+(4*4)+5*3)>
• Crosswise multiply and add the last 3 digits <(3*6)+(4*5)+(5*4)>
• Crosswise multiply and add the last 2 digits<(4*6)+(5*5)>
• Vertical multiplication of last digits (5*6).

The final answer for the above equations using the carry forward method will be 8104320

Share with your friends