The foundation of many areas of Mathematics emerged from the brilliant nation of India. Vedic Math Sutras or Indian Mathematics commenced around 1200 BC and lasted up the later part of the 18th century until modern technology and methods took over.
Important contributions were made in this area by scholars like Aryabhatta, Brahmagupta, Bhaskara II, Varahamiriha. The concept of zero as a number, negative numbers, the decimal system, and a lot more find their roots in Vedic mathematics. The concept of Trigonometry, the sine and the cosine also developed further, thanks to this interesting subject. Read about the advantages of learning Vedic Maths, here.
This article will help you learn and apply the first and the most crucial Vedic Maths Sutra- The Ekadhikena Purvena.
The Genesis of Vedic Maths
All ancient and medieval works were composed in Sanskrit and it usually contained sutras (rules) which aided students with memorization. It was also followed by a prose commentary section that provided detailed justification of all problems. The oldest mathematical document is the BAKSHALI MANUSCRIPT discovered in 1881 in modern- day Pakistan which is stated to be likely from the 7th century CE.
Indian mathematician and monk Shri Bharati Krsna Tirthatji believed that there are 16 sutras in Vedic Maths. Check out the other sutras like the Paryavarta Yojayet over here!
We will now have a look at the very first of these 16 sutras. This sutra is called the Ekadhikena Purvena.
Vedic Maths Sutra 1- Ekadhikena Purvena
The term ‘Ekadhikena Purvena’ means- ‘by one more than the previous one.’
Ekhadhikina Purvena is a method useful for finding the squares of numbers and special divisions like 1 divided by a number for eg: 19, 29, etc.
Using the conventional method, it is difficult to divide 1 by numbers ending with 9 like 19, 29, 39. This is so because some of these are prime numbers and thus cannot be factorized. To reduce such tedious tasks as well as mistakes we apply the sutra Ekadhikena Purvena.

Method 1 – Going from left to right
Suppose we take 1 divided by 29, 1 being the numerator here and 19 being the denominator (1/19).
For the denominator 29, the Purva or the first digit of the number is 1.
Hence, the Ekadhikena Purvena for this i.e one more than the previous will be
1+2=3.
Now we will be using 3 as the denominator for the division purpose i.e 1/29 = 1/30 yet they are not equal
- Divide 1 by 3 and it will give a quotient of 0 and 1 as the remainder.
- Now, the quotient and remainder are collectively 10. Divide 10 by 3. This gives a quotient of 3 and a remainder of 1.
When we are writing these numbers it will appear something like this:
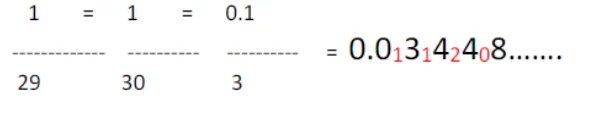
- Again, we divide 13 by 3. This will give us a quotient of 4 and a remainder of 1.
- Similarly, we continue the same process till we get the same quotient and remainder we found at the very first. This means the Quotient is 0 and remainder is 1.
And our final answer will be the series written in black.
Once you grasp the concept, it becomes easy to divide such numbers.
Method 2. – Go right to left
This is also the Ekhdikena Purvena. The difference here is just that we use the 3 for the multiplication process instead of division.
Therefore,
- We will start by taking the number 6 (considering this was the last number in the division process given above) and multiply it by 3. This gives 18.
- Now write 8 on the left side of 6(now that our process is from right to left) and carry forward the 1.
- Now multiply 8 by 3(as 3 is our Purva for the division) by 8 and add 1 which gives 25.
- Again, write on the left of 8 in the series and carry forward the 2.
- Continue this process. Keep doing this till you get your desired number or the same pair of quotients and remainder is obtained as earlier.
Our final answer is our series written in black.
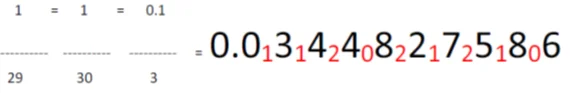

Let us take another example to be clear with our concepts:
We will now take 38/59. This can be approximated as 38/60 and can be further written as 3.8/6. We will be following method 1.
- So our numerator is 3.8 and denominator is 6. This gives us a quotient of 6 and remainder as 2.
- Now as our quotient and remainder are collectively 26 dividing it by 6 gives a quotient of 4 and remainder of 2.
- Keep writing it in a series so that you don’t forget it.
- Now divide 24 by 6. This gives you a quotient of 4 and a remainder of 0.
- Continue the series until you get the desired number.
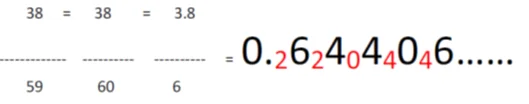
WHEN THE NUMERATOR IS GREATER THAN THE DENOMINATOR
Suppose we have to divide the number 12345 by 39. In the previous methods, the numerator and denominator had an equal number of digits. Here, however, the numerator is greater than the denominator. Hence we need to apply a different method. This can be a little tricky but it is fun when understood.
- Let us take 12345 divided by 29. This is approximated to 12345/30 = 1234.5/3
- For the first division, we will simply divide 12 by 3. This gives us a quotient of 4 and a remainder of 0.
- Now we still have 3 digits (34.5) left in the original dividend which is 123.45.
- Therefore we will now add 4 (from our series) to 3 (the first digit from the original divisor) which gives us 7.
- Now divide this 7 by 3 which will give us a quotient of 2 and a remainder of 1.
- Again add the quotient (2) which the next digit in the original dividend which is 4. This gives us 6. Now append the remainder 1 from the series with 6.
- Hence the next number to be divided by 3 is 16. This gives the quotient as 5 and the remainder as 1.
- Again add the quotient 5 from the series to the next remaining digit 5. This will give us 10. Now append the remainder 1 to it. In this case, we put 1 in the ten’s place while adding, so instead of 11+1=12 we will get 11+10=20.
- So now we divide 20 by 3. This gives us a quotient of 6 and a remainder of 2.
- From here onwards the division takes place normally as we did in Method 1.

These Vedic Math methods are quite helpful even in this modern day and age. Learn them with a little patience and then perform calculations in seconds!
Share with your friends