Polygon – this six letter word has a lot to offer! When we are about to extract an in – depth understanding of polygons, let’s begin with imbibing this simple fact that there’s lot more than seeing it as just a figure constructed completely of line segments. So, what’s the wait for? Let’s dive into this article and build a clear understanding of Polygons. Hold on, that’s not it! This article also aims at simultaneous strengthening of concepts and clarification of doubts.
Polygon : Definition
First things first, cutting the absolute non – essentials, let’s begin with talking about what a polygon is. In geometry, we define polygon as a two – dimensional figure with a fixed number of edges. These edges are the sides of the figure which are connected from joint to joint or end to end. Further, it’s this meeting point of line segments, which we address as a vertex or a corner. Henceforth, that’s how an angle is achieved.
Often at times, one can consider all two dimensional figures as polygons but it’s not the case. All polygons are two – dimensional figures, but not the vice versa is true. Before moving ahead know that the word polygon is comprised of two words meaning poly (many) and gon (sides).
Names of Polygons
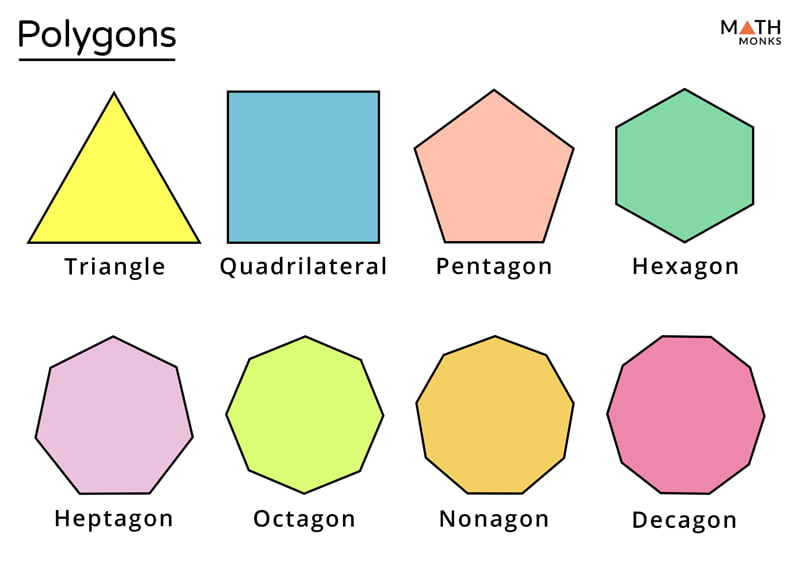
Polygons get their names from the prefixes of ancient Greek numerals. Many names of ordinary objects and concepts begin with the Greek number prefix. These can be helpful in remembering how many sides a polygon has on occasion. The number of sides, e.g., pentagon, dodecagon, by combining a Greek-derived numeral prefix with the suffix -gon. The exceptions are the triangle, quadrilateral, and nonagon.
Mathematicians frequently utilize number notation, such as 17-gon and 257-gon, in addition to decagons (10-sided) and dodecagons (12-sided).
Side counts that are easily articulated in verbal form (e.g., 20 and 30) or utilized by non-mathematicians are exceptions. Some unique polygons have their own names, such as the regular star pentagon, which is also called the pentagram.
Consider the following scenario:
An octagon has eight sides, just like an octopus.
A decagon has ten sides; hence a decade is ten years.
The contemporary pentathlon consists of five events, similar to the five sides of a pentagon.
Seven events make up an Olympic heptathlon, much as a heptagon has seven sides.
The word ‘poly-‘ simply means ‘many,’ therefore a polygon is a form having numerous sides, similar to how ‘polygamy’ refers to several wives.
For the purpose of creating higher-level names, Combine the prefixes as follows to create the name of a polygon with more than 20 but less than 100 edges. Although not all sources use the name “kai,” it was used by Kepler and supported by John H.
Also, Read The CGPA Grading System and All You Need To Know About It
Types of Polygon Angles
There are two sorts of angles in a polygon:
- Interior angles – Angles created at the vertices of a polygon’s vertices.
- Exterior angles – Angles are created when a polygon’s side is extended outside the polygon. It’s next to (to the side of) the internal angle.
Polygonal Shapes
Polygons are of numerous types based on their sides and angles, such as:
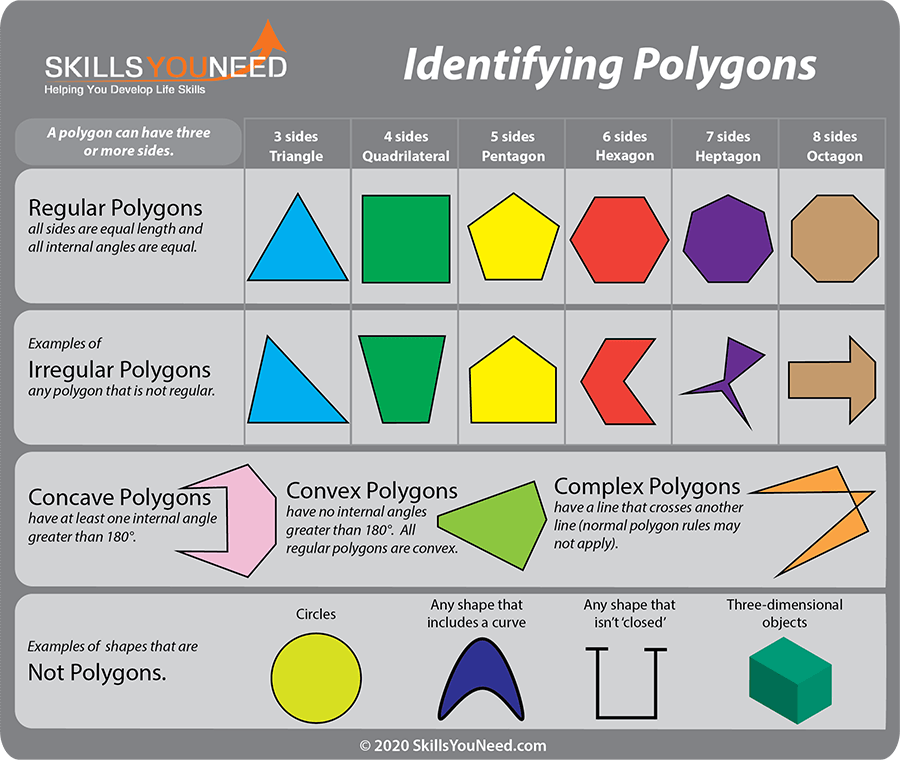
Regular Polygon
A regular polygon is one in which all of the sides and interior angles of the polygon are equal. Squares, rhombuses, equilateral triangles, and other regular polygons are examples.
Irregular Polygon
An irregular polygon is the one in which all of the sides and interior angles have distinct measurements. A scalene triangle, a rectangle, a kite, and so on.
Convex Polygon
A polygon that is convex is a convex polygon is defined as one in which all of the internal angles are strictly less than 180 degrees. From the center, the vertex will point outwards.
Quadrilaterals
Quadrilaterals are polygons with four sides, however quadrilaterals with the same side and angle sizes are referred to as squares. A rectangle is a polygon with four right-angled corners and two opposing sides that are longer than the other pair of sides.
There are three types of triangles, each with its own name:
An equilateral triangle is a regular triangle with the same size sides and angles on all sides.
An isosceles triangle is a triangle with an uneven form.
The right-angle triangle gets its name from the fact that one of its angles is a right angle.
Regular polygon
Euclidian geometry supports that a basic polygon can be understood as an equiangular. this term means that al the angles of the polygon will be equal when they are measured. Euclidian geometry also discusses how a basic polygon can also be called an equilateral polygon. this means that all the sides of this polygon the same length. Convex or star-shaped polygons can be found in regular polygons. A succession of regular polygons with an increasing number of sides approximates a circle in the limit or a regular apeirogon (basically a straight line) in the limit if the perimeter or area is fixed.
Irregular polygon
Irregular polygons are those that do not have equal sides and angles on all sides. In other words, irregular polygons aren’t the same as regular polygons. Polygons are two-dimensional closed figures made up of three or more-line segments joined together. Regular and irregular polygons are the two forms of polygons.
Irregular Polygon Properties
Irregular polygons have a few unique characteristics that set them apart from other polygons. The properties are as follows:
- The sides and angles of an irregular polygon are not equal.
- In nature, irregular polygons can be convex or concave.
- Irregular polygons can be shaped in a variety of ways, both simple and sophisticated.
- Irregular polygons have endlessly huge sides because their lengths are not equal.
- Because the adjacent sides and angles of irregular polygons such as parallelograms, trapeziums, and quadrilaterals are not equal, they are classified as irregular polygons.
Irregular and Regular Polygons: What’s the Difference?
Based on the length of its sides, a polygon can be classified as either regular or irregular. Regular polygon, as the name implies, refers to a certain pattern that exists in a regular polygon, whereas irregular polygon refers to an irregularity that appears in a polygon.
Triangle
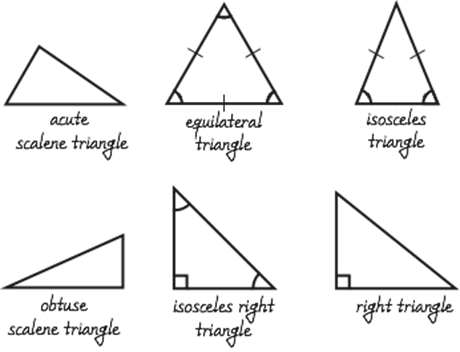
Triangles are polygons with three sides.
A triangle is a three-sided polygon. There are various sorts of triangles (as shown in the diagram), including:
All of the sides have the same length, and all of the interior angles are 60 degrees.
All of the sides have the same length, and all of the interior angles are 60 degrees.
have two equal sides and a varied length on the third. There are two internal angles that are equal.
has three separate sides and three different internal angles. Internal angles are another way of describing triangles (see our page on Angles for more about naming angles). A triangle’s internal angles always add up to 180°.
An acute (or acute-angled) triangle is a triangle with solely acute internal angles. Obtuse (obtuse-angled) is a shape with one obtuse angle and two acute angles, while acute (acute-angled) is a shape with one obtuse angle and two acute angles.
Also, Read Education Boards like CBSE, ICSE, IB and More
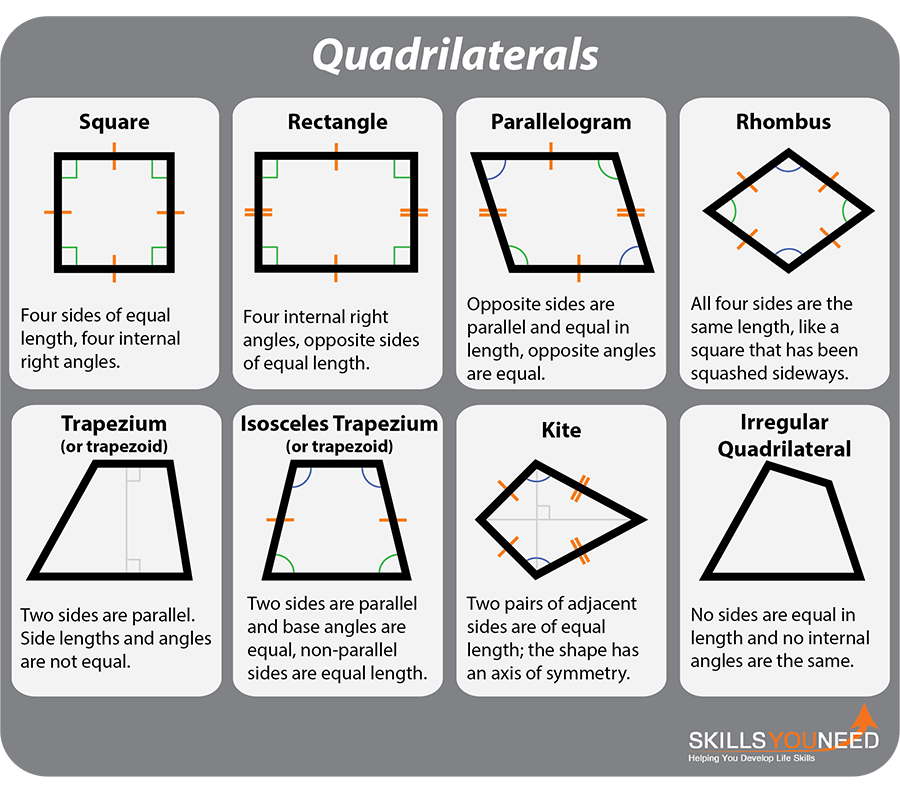
Quadrilaterals
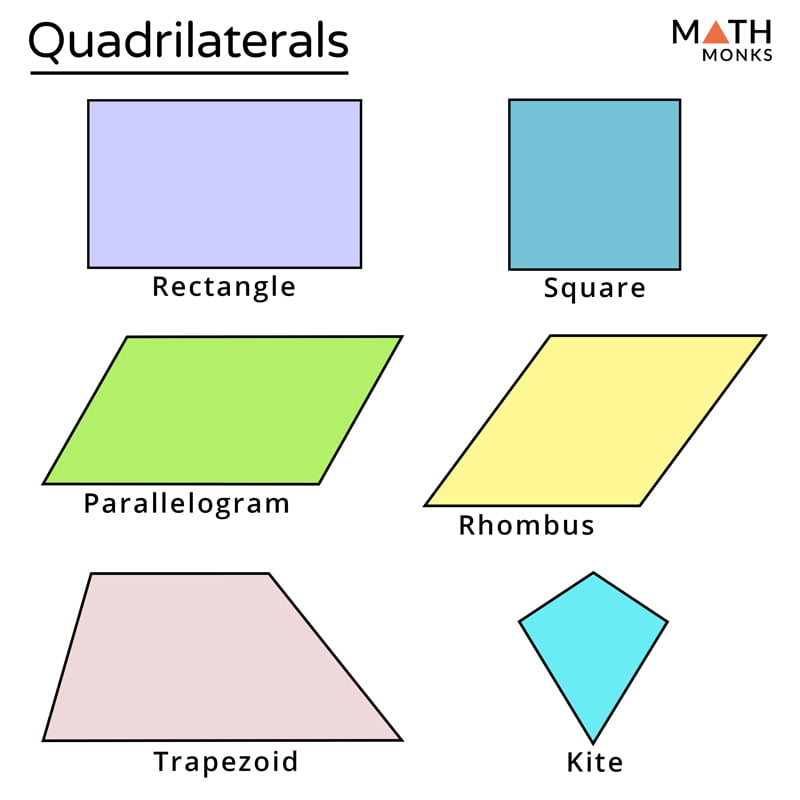
These are polygons with four sides. Quadrilaterals, quadrangles, and tetragons are all terms used to describe four-sided polygons. People use the term quadrilateral very often in geometry.
‘The freshers gathered in the college quadrangle,’ for example, is a common use of the term quadrangle to indicate a rectangular enclosed outdoor place. The terms tetragon, polygon, and pentagon are all interchangeable. It is pretty uncommon to stumble across it, although people do not often utilize it in practice.
The square, rectangle, rhombus, and other parallelograms, trapezium/trapezoid, and kite are all members of the quadrilateral family.
All quadrilaterals’ internal angles sum up to 360°.
- Square Four equal-length sides and four interior right angles make up a square.
- Rectangle: Four internal right angles with equal length opposite sides.
- Parallelogram: The opposite sides of a parallelogram are parallel, the opposite sides are equal in length, and the opposite angles are equal.
- Rhombus: A form of a parallelogram in which all four sides are the same length, similar to a square turned sideways.
- Trapezium: Two sides of a trapezium (or trapezoid) are parallel, but the other two are not. Angles and side lengths are not equal.
- Isosceles Trapezium (or trapezoid): Two sides are parallel, and the base angles are equal, so non-parallel sides are the same length.
- Kite: The shape features an axis of symmetry, with two pairs of adjacent sides of equal length.
- Quadrilateral Irregular: a four-sided shape with no straight edges.
Area of Polygons
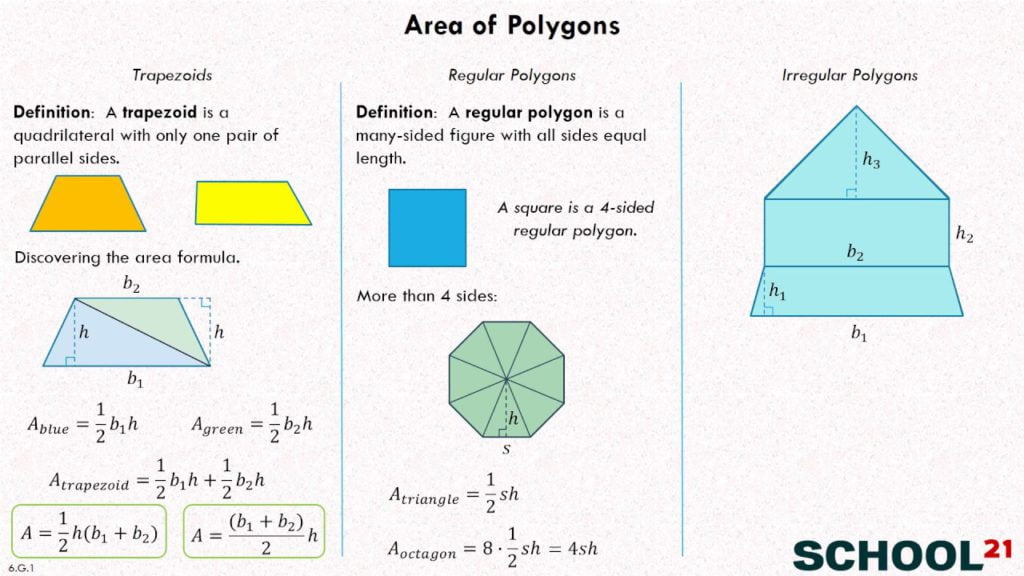
The quadrilateral is the simplest and most fundamental polygon for determining area. To get the area, multiply the length by the vertical height.
Note that the vertical height of a parallelogram is the vertical distance between the two horizontal lines, not the length of the sloping side.
This is due to the fact that a parallelogram is simply a rectangle with a triangle clipping off from one end and is now on the other:
The rectangle becomes a parallelogram when the left-hand blue triangle is removed and replaced on the opposite end.
One can calculate the area by multiplying the length (the top horizontal line) by the height (the vertical distance between the two horizontal lines).
Also, Read Fun and Easy Festive Crafts For Kids
History
Polygons have been around since the dawn of time. Regular polygons were known to the ancient Greeks, with the pentagram, a non-convex regular polygon (star polygon), appearing on a krater by Aristophanes, discovered in Caere and now in the Capitoline Museum, as early as the 7th century B.C.
In the 14th century, Thomas Bradwardine published the first comprehensive study of non-convex polygons in general. To generate complex polygons, Geoffrey Colin Shephard adapted the notion of polygons to the complex plane in 1952, where each actual dimension is complemented by an imagined one.
Polygons in Nature

Polygons are visible in rock formations, most typically as the flat facets of crystals, with the angles between the sides varying depending on the material.
Regular hexagons can develop when lava cools, forming regions of closely packed basalt columns, as seen in the Giant’s Causeway in Northern Ireland and the Devil’s Postpile in California.
In biology, the wax honeycomb formed by bees has an arrangement of hexagons on the surface, and each cell’s sides and base are likewise polygons.
What is the best way to memorise polygon names?
Triangle
Triangles have three sides, so we may recall them by picturing a three-wheeled tricycle. The “tri” at the start of the tricycle is the same as the “tri” at the start of the triangle. A piece of pizza, traffic signals, and a billiards rack are all instances of triangles in real life.
Quadrilateral
Quadrilaterals have four sides, therefore quad motorcycles with four wheels come to mind. A deck of cards, a chessboard, and books are all instances of quadrilaterals in the real world.
Pentagon
Pentagons have five sides, and we use five fingers to wield a pen. The black portions of a football, a pencil, and okra are all examples of pentagons.
Hexagon
Because hexagons have six sides, we may concentrate on the “x” in “hexagon” and the “x” at the end of “six.” Honeycomb and metal nuts are two instances of hexagons in real life.
Septagon
Septagons have seven sides, and because “sept” sounds close to “sev,” we may call them “seven-agons.”
Octagon
We can imagine an octopus with eight tentacles since an octagon has eight sides. An open umbrella is an example of an octagon in the real world.
Nonagon
Nonagons have nine sides, and their name sounds a lot like “nine-again”! The US Steel Building in Pittsburgh, Pennsylvania, is a real-world example of a nonagon.
Decagon
There are 10 sides to a decagon, and ten years make up a decade. Australia, Belize, and Hong Kong are among the countries that use ten-sided coins.
Terminologies related to Polygon
Sides: The polygon sides are the line segments that constitute the polygon’s exterior.
Adjacent Sides: Two sides of a polygon with the same endpoint are next to each other.
Vertex: The vertex of a polygon is the point at which the sides of the polygon meet. It is also the end-point. Vertices are the plural form of vertex.
Adjacent Vertices: Adjacent vertices are the endpoints of the same side of a polygon.
Also, Read Communication Skills- How to Communicate Effectively
FAQs
Q. What are the fundamental geometric shapes?
Answer: A fundamental geometric shape is a figure or area that is bounded by a border formed by uniting a specific number of curves, points, and lines. Triangles, circles, squares, rectangles, and other fundamental geometric forms include triangles, circles, squares, and rectangles. We are all familiar with the basic forms in geometry, but there are many more.
Q. What is the name of a three-sided shape?
Answer: A triangle is a three-sided shape with three sides. Triangles are generally polygons with three sides. Be a result, any polygon with three sides is what you call a triangle. In geometry, the triangle is one of the most common fundamental forms.
https://www.youtube.com/embed/MPYNEYeLYaQ?feature=oembedWhat is a polygon?
Q. What is a polygon with seven sides called?
Answer: A Heptagon is a polygon with seven sides. There are 7 vertices in this polygon.
Q. What do we call a polygon with nine sides?
Answer: Nonagon is a polygon with nine sides. There are 9 vertices in this polygon.
Q. What is the number of diagonals in a polygon?
Answer: A polygon with n sides (sometimes known as an n-sided polygon) will have n(n – 3)/2 diagonals. There are no diagonals in triangles.
Q. What are the many polygon types?
Answer: There are four types of polygons. They are as follows:
Regular polygon – all sides and interior angle measurements are the same.
Q. Irregular polygon – all sides and interior angle measurements are not equal?
Answer: A convex polygon is one in which all of the internal angles are smaller than 180 degrees. From the centre of the form, the vertex will point outwards.
One or more internal angles of a polygon are more than 180 degrees, making it a concave polygon. A concave polygon must have at least four sides to be a concave. The vertex is pointing towards the polygon’s interior.
Q. What is a trapezoid’s shape?
Answer: A trapezoid is a form that has four sides and at least one set of parallel sides. It can also be a parallelogram if it has two parallel sides. If two sides are not parallel, however, the trapezoid is merely a basic trapezoid.
Q. Is a Regular Polygon a Rectangle?
Answer: All of the sides of a regular polygon are equal. Polygons are three-dimensional figures with more than two sides. Polygons have names based on the number of sides and angles they have. The triangle, rectangle, square, and other polygons are the most well-known. As a result, a rectangle is also a regular polygon.
Q. How do you calculate the area of a polygon with n sides?
Answer: We divide the figure into triangles, squares, trapeziums, and other shapes to calculate the area of a polygon that is not regular or whose formula is unknown. The goal here is to display the supplied geometry as a collection of geometries for which we can compute the area.
Also, Read Article Writing and How To Improve Your Skills!
Share with your friends






