The Latin word “Angulus”, which means an angle, is the root of the word “angle”. In other words, Angle is a figure that is formed from two lines or rays single common endpoint. You can see different types of angles in your environment. For example, you can see the intersection of roads and the angle of trees to the ground.
In addition, We also use angles to measure a change in the trajectory of motion of objects in motion such as ships, planes, and stars. There are many other applications of geometry, and the concept of angles is an important tenet. This is why Mathematics students must study angles early in their studies.
Here are two types of ranges based on rotation wise if the rotation of the angle is in an anticlockwise direction, that will be called the negative angle, and if the angle moves in the clockwise direction it’s called a positive angle.
There are many types of angles in geometry: right angle, reflex, right angle, an acute angle. An acute angle is an angle less than 90 degrees and an obtuse one is one greater than 90 degrees. There are also special types of angle pairs. We will be learning about the different angles in mathematics.
Let’s see How an Angle looks like
When two rays emanating from the same point create Angle, these rays create the angle known as the arms or the Angle. The vertex is their origin point. The representation of an angle is ( ∠ ).
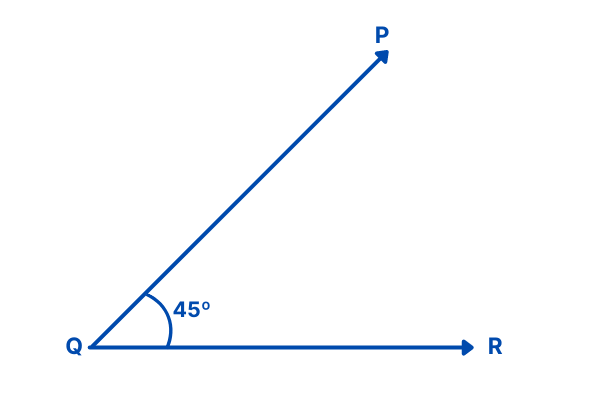
Image Source – Google
you can see in the above diagram, angle ∠ PQR Formed at Q. Here the same angle represented as ∠RQP
∠QRP. Here the Angles are measured by deg (0)
The rays above combined in many ways to create different angles. Let’s begin by looking at these types of angles.
Different Types of Angles in Math and Geometry
Geometry invented the concept of angle. The concept of angles is used in different areas in our day-to-day life like design, architecture, and selection of construction material. It is an essential part of the technical background that allows for various designs, manufacturing, blueprints, programming, and many other things.
You can see geometry in the way they constructed different shapes in a particular way in ancient times. Angle is derived from the Greek words for “ge” (which means earth and measurement), in this way the term geometry arrives.
This article will focus on angles and the various types that are based on their measurements.
There are many types of angles in nature. Each one is important in our day-to-day lives. Engineers and architects use angles to design machines, roads, bridges, and buildings.
Athletes use angles in sports to improve their performance. To throw the ball far and quickly, one must spin the disk at a specific angle. To pass the ball from one player to another in soccer, you need to use a specific angle.
Artisans and carpenters use angles to create objects like sofas, tables, chairs, tables, pails, etc. Artists use to draw portraits and paint. Fashion designers use angles to ensure that they have the most flattering outfits. It is important to learn about the various angles.
Based on Measurement
The following classifications are based on angles’ measurement. The following illustration shows the relationship between the various types of angles.
Here are 6 types of angles in Geometry which are based on Measurement
Acute Angle
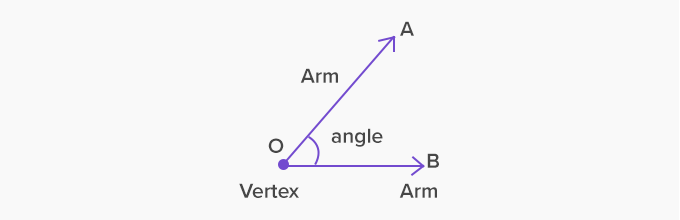
An acute angle is an angle measuring between 90deg to 0deg. It is smaller than a right angle (an L-shaped shape), but still has some space between the lines that make it. An acute angle is a “V” shape.
An angle refers to the area between two intersecting lines or planes (surfaces), and the figure that results from such an intersection. These are not the same as the temperature measurements.
Why is the Acute angle important in Geometry?
To measure the angle you can use a tool name Protractor. You probably used a protractor to measure angles. There are three main types of angles: right angles, obtuse and acute.
The four corners inside a square are the angles. All of these angles measure 90 degrees. These angles are all right angles (each measuring 90deg).
Understanding the differences between angles is one of the most important lessons in geometry. Once you grasp this concept, you can move on to more complex concepts. The essential aspects (right and obtuse) are crucial in many fields that depend on the geometry and exact measurements of shapes. It is very amazing when you see every corner of your home you will find out the angles when you see corner of your home.
Right Angle
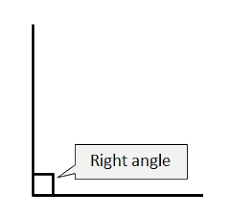
A right angle is one with a 90-degree measurement. This is the most common angle we see in our daily lives. You can see it in corners, boxes, ledges, on the screen of your mobile phone, and in other places. A rectangle and a square always have right angles with one another. This article will provide more information.
A right angle is an angle that measures 90deg. When the two rays intersect and that is perpendicular at the intersection then the right angle is formed. They take the form of the letter L. The following illustration shows that ray AB, BC, and ray AB form a right angle ABC.
The right angle is similar to the alphabet L. You can see it in many forms, such as the angle made at 3:00 p.m., The edges of a door., Television’s four edges, Corne of the chair., Mobile screen
You can measure the Right angle with Protractor
One of the tools used to measure a right angle is protractors. You can use a right-angle calculator To determine if the angle given is right or wrong. The angle has checked the sides and corners of the set squares to the angle. To verify that the angle given matches the shape of the sides, we also use a test square. The protractor’s baseline should match the base of the unknown angle. Next, we verify that the angle’s other ray passes the 90-degree mark. If the ray passes the 90-degree mark, it is at a right angle.
Obtuse Angle
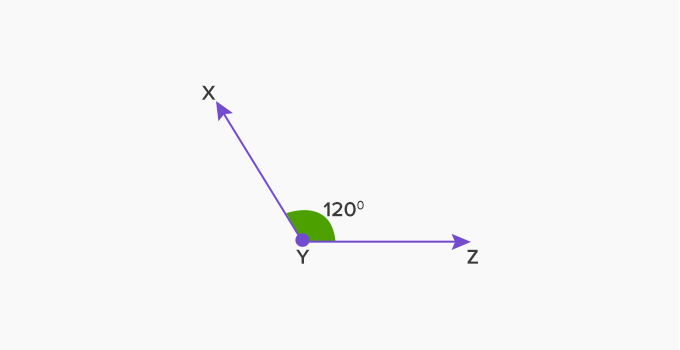
An obtuse angle refers to one of the angles found on a plane’s surface. An obtuse angle in Geometry is more than 90 degrees and less than 180 degrees. Many times, we can see clocks that frame many obtuse angles degrees in between one minute and one hour. This happens often during 24 hours. We will explore the properties of the obtuse angles and learn more.
What is an Obtuse Angle?
An obtuse angle is an angle that measures greater than 90deg or less than 180deg in Geometry. The combination of a straight and right-angle leads to the formation of an Obtuse angle.
Obtuse Angle Degree
The examples of obtuse angle degrees are 165deg,135deg,110deg,189deg, 91deg. The obtuse angle degree is therefore within the range of 90deg to less than 180°.
Examples of Obtuse Angles
Obtuse angles are angles that measure greater than 90 degrees and less than 180 degrees. Talk about the example of obtuse angles that measure145°,150°,178°,149°, 91°.
Here is Real-Life? Examples.
Did you ever notice the bizarre angles you can see around you? There are many examples.
- The hands of this clock are quite striking. Because it measures between 90o to 180o, the angle formed by clock hands is obtuse. Analog clocks have more examples of times when the clock hands create obtuse angles, such as 3:35. Are there more? Please leave comments!
- The ballerina can stretch her legs to an amplitude characteristic of an obtuse angle. She can maintain her balance and amplitude. If she turns to the opposite side, the angle will still be the same.
- A pizza eaten by more than one-quarter of a person, but not the entire amount. An obtuse angle is what is missing from the pizza.
- The fan is open completely and forms an obtuse angle. If it is slightly closed, it’s formed right angle. However If it is more closed, but not completely, it is an acute angle.
- Because the angle of the excavator’s arm is obtuse, it can dig deeper into the soil than if it had a smaller angle.
Straight Angle
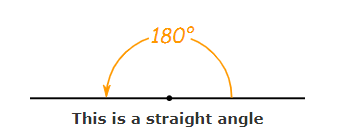
Straight angles measure 180deg. They look like straight lines. It is an angle where the arms are in opposite directions to the vertex. They join together to form 180deg.
A straight line is defined as when two rays are joined together. The angle formed when the intersection of two rays in opposite directions and two rays from one direction. A straight angle in geometry is an angle whose vertex points have a value of 180 degrees.
Now when is an angle straight?
An angle is defined as two rays from the same direction on opposite sides of a point. They form the shape of a line.
Straight angles are when a ray does a half-turn around a point, however, it ends in the same place but points in the opposite direction. This means that if you stand looking at a door, and you turn 180o, it will be behind you. When someone completely changed their mind, they are called a “180”. If a friend says that cats are their favorite animal, but another day doesn’t like them, we can call it a 180.
Examples of straight angles in day to day life
It is easy to find this information by reading the hours of an analog clock. What times does the clock hand form a straight line? Straight angles seen when you stretch your arms and dancers stretch their legs.
Reflex Angle
A reflex angle is an angle between 180 0 to 360 0. The reflex angle and the angle on the opposite side formed 360 0.
Reflex angles are always larger than straight angles that are half-circles (180 0 ), or complete angles which are full circles (360 0 ). A reflex angle has an acute angle and an obtuse or right angle.
Reflex Angle Diagram
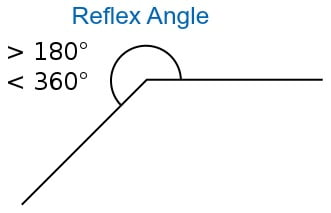
An angle is a measurement of the distance between two lines that intersect at a point. Let’s take A, B, or O as examples to identify the angle. The following illustration will show you the reflex angle. The larger angle is acute. To avoid any confusion, we refer to the outside angle as reflex AOB.
Real-Life Examples of Reflex Angle
- Clock: When we look at the hands of a clock, it is obvious that one side of the clock has an odd angle. This is the side that falls on the numbers 7, 8, 9, 10, 11, 12, as indicated in the clock. In the opposite side, which has the numbers 1, 2, 4, 5, 6 formed reflex angle.
- Pizza: If we cut a small piece of pizza and take it out, the rest of the pizza will form a reflex angle.
- Table: A rectangular table forms a 90deg right angle with its top (90deg) and its leg. The outer angle formed by the same top as the leg is a reflex angle at 270deg.
Full Rotation Angle
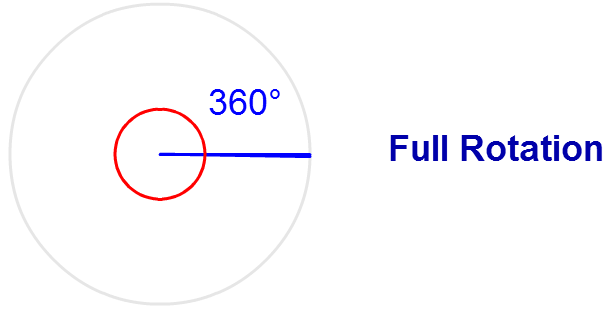
A full rotation angle occurs when one arm of the angle makes a complete turn or a 360deg. You can see in the above figure the full rotation angle or 3600
Types of Angles based on Rotation
The direction of rotation for one angle arm is the next type of angle. As I mentioned above about the angles. Let’s discuss the different types of angles based on rotation.
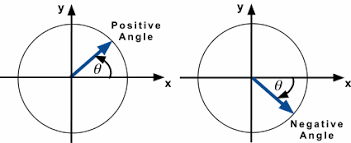
Positive Perspectives
A positive angle is Formed when the angles are rotated from the base in the anti-clockwise or counter-clockwise direction. You can see in the above figure above shows that the side can be rotated in an anticlockwise direction by angle th. This creates a positive angle.
Negative Angles
Negative angles are those in which angles are rotated in the clockwise direction from the base. In the above figure you can se that if the side is rotated clockwise by an angle, a negative angle will be formed.
Types and Combinations of Angle Pairs
A pair of angles is a combination of two angles. Let’s learn more about the different angles pairs in geometry.
Adjacent Angles
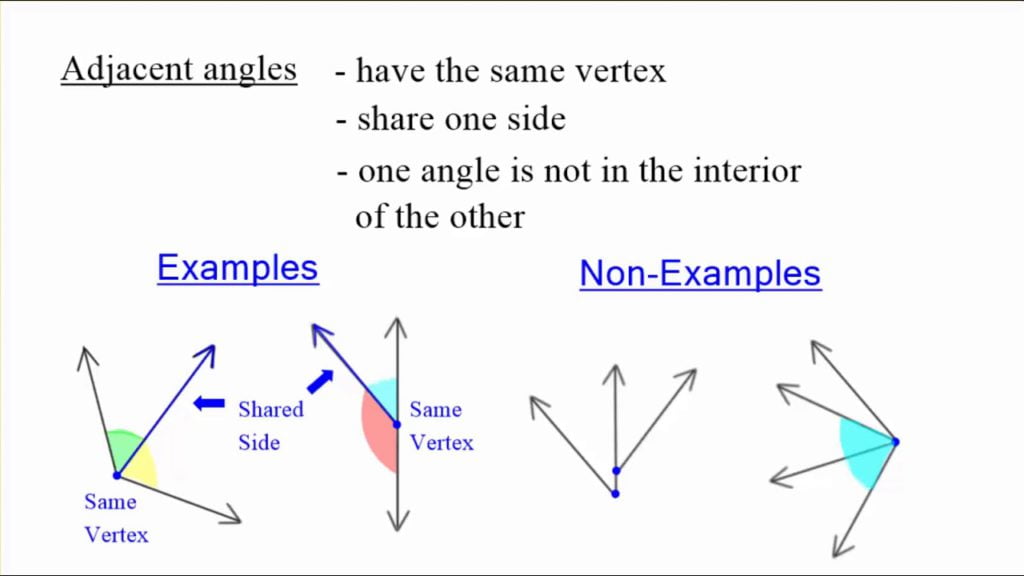
The following conditions must be met for line the two angles to be adjacent.
- Two angles share the same vertex.
- Two angles share one arm.
- Two arms are not commonly used.
Complementary Angles
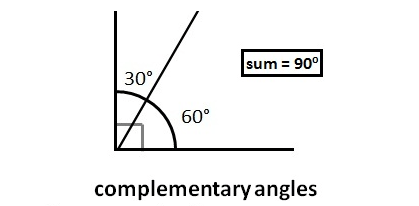
Complementary angles are two angles whose sum is greater than 90deg. You can have two angles of any length that add up to 90deg. The two angles could be, for example, 30deg or 60deg.
Supplementary Angles
Supplemental angles can see when the sun of two angles is greater than 1800. When the two angles are added together, they make 180deg. For example, 180deg is made up of 110 0 + 70 0, These two angles are referred supplementary. One angle is the complement of another one. The 60deg supplement is, for example, 180 0 – 60 0 . 120deg is the equivalent.
Alternative Interior Angles

Alternate interior angles are formed when a line for line or a transversal passes through two parallel lines.
Alternative Exterior Angles
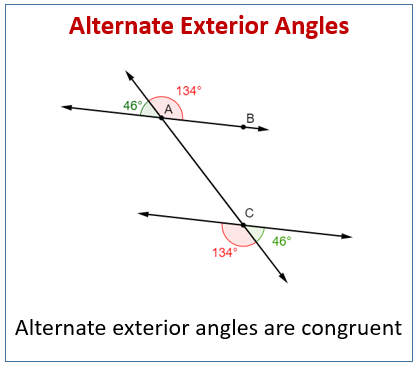
Alternate exterior angles are two angles that are on opposite sides of the transversal. They are placed on two lines. If the lines are parallel, these pairs of angles will always be equal.
Corresponding Angles
A line or transversal crosses two parallel lines angles at the same place or side of the transversal will be corresponding angles. These angles are congruent.
Vertical Angles

Verticle angle is when two lines intersect, and the angles that are opposite each other are equal. This is known as vertical angles or vertically opposing angles.
Wanna know about the guide for kids to be problem solvers click here
What are the 7 types of angles in maths?
Angles are measured in degree ( 0 ), here are 7 types of angles zero angles, acute angles, right angles, obtuse angles, straight angles, reflex angles, and complete angles.
What are the 12 types of angles?
On the basis of Measurement and Rotation, there is a total of 12 types of angles you can open to read it out.
What is a 360 angle called?
360 angle also called full rotation angle, A full rotation angle occurs when one arm of the angle makes a complete turn or a 360 0 . The figure shows MNR = 3600. this is called the full-rotation angle.
History of Types of Angles in Math and Geometry
Since over 2000, the nature of the angle concept has been the subject of much debate. The discussion continues for many years (Matos 1990). Maybe that is why? no one accepted the definition by the mathematical community. Dominant transposition is not an easy task. Michelmore and White, 2000, This peculiarity is called the multifaceted nature and concept of angle, it is composed of the related contexts in which the angle is situated. Physical situations These authors can use diverse textbook definitions.
Different formal mathematical structures exist, meanwhile there is no clear definition. Coinciding with all of the physical contexts of an angle emphasizes the difficulty in Forming a general standard concept. Casas (2000) included historical elements in his research on the notion. These articles were based mainly upon Matos (1990 and 1991). They are not the only examples. Describe the reasons for the student’s conflict. The cognitive plane is an explanation that can be found in Michelmore and White (1995, 2000), arguing that cognition is located.
Relates to the didactic plane (the outcome of didactic transposition), but leaves out, however, A description of the role that mathematical knowledge plays in this scenario, also the epistemological nature and meaning of the idea of angle. These studies provide some historical ideas but do not reflect on the actual events.
Epistemology concept does not include the notion of angle. If a mathematical object is made scholar, it retains or loses its significant knowledge. The cognitive component of didactics is the focus of the authors.
phenomenon and how it relates to scholarly discourse structure. According to the Concept of angle, elements concerning their epistemological nature can be identified. This is based on the Matos notes (1990 & 1991). Not only the historical evolution but also the stages and phases of construction.
History and construction of angle
Matos created a historical account of the concept ‘angle’ to understand its origins, properties, and the difficulties that he faced. This concept is for both successful and unsuccessful people.
Although in his last discussion of its nature, Matos does not report a consensus from the scientific community.
Use of the Notion of Angle
It is important to distinguish between the use of and the application of the term. The first will show that angle is an important part of certain activities. However, it is still a notion. Application refers to applying the formal concept to the situation. This is why angle becomes so important in school contexts. Students can develop intuitive concepts that define the angle.
Construction and Astronomy were the appropriate contexts for the use of the notion of angle. They were underlying the direction and inclination of celestial bodies, constructions, and had a meaning that would later become geometric objects.
Pre-Columbian Maya built structures to create celestial phenomena. There are 365 steps in total, which is the number of days in one year. The total number of steps in the four stairways is 365, which is the number of days per year.
Measurement of time, which is one of many purposes of astronomy across cultures (Babylonian and Hindu, Chinese, Maya among others), was a significant step forward. It was an easy step to establish the day-to-night transition as the benchmark for time measurement. Then, it was possible to observe the movements of the sun or moon.
These phenomena were not enough to determine the best time to do the activities of each community (agriculture and fishing, navigation, and trade). Therefore, the observation and recording of the changing positions and planets led to the need for better tools and references.
Some of the most noteworthy contributions to the practice of astronomy and geometry-trigonometry are the division of the circle into 360 parts, the arc-chord tables equivalent to today’s trigonometric tables, and information on the positions of the stars, which would later serve as validation for the first geometric models.
Identifying the Angle
It is important to distinguish between the use of the term and its application. The first will show that angle is an important part of certain activities. However, the application refers only to applying the term to a situation.
Astronomy and construction were the right settings for the idea of angle. The orientation and direction of a celestial body and constructions give them meanings that can be later be given to geometric objects.
Pre-Columbian Maya built structures to create celestial phenomena. Each of the four stairways in the structure has 365 steps. This is the number of days in a calendar year.
Measurement of time, which is one of many purposes of astronomy across cultures (Babylonian and Hindu, Chinese, Maya among others), was a significant step forward. It was natural to measure the time change from day to evening as the first benchmark. However, this would not be enough to determine the best time to do the activities of each community (agriculture and fishing) so observation and recording the changes in the positions of the planets and stars began. This led to the need for better tools and references.
Some of the most noteworthy contributions to the practice of astronomy and geometry-trigonometry are the division of the circle into 360 parts, the arc-chord tables equivalent to today’s trigonometric tables, and information on the positions of the stars, which would later serve as validation for the first geometric models.
Frequently Asked Questions
- Why do we need angles?
Angles are used in our daily life incidents. From architects to engineers to astrologers, most of the professional work involves use and understanding of angles. Hence, understanding these angles becomes important.
- What is F Rule in Angles?
In actuality, the angles which lie at identical positions on each parallel line would also be equal to the angle in that position on the other parallel line. This rule can sometimes remembered as “F angles” because the angles make an F shape.
- How many parts are there in an angle?
An angle specifically consists of three parts : 2 arms and 1 vertex.
Final Thoughts
This article talks in detail about the various types of angles. Getting the concept thoroughly clear acts as the first step at excelling at a particular topic and heading on to scoring good in exams. Go over the Podium Blog, for capturing enthralling details on more such topics.
Share with your friends